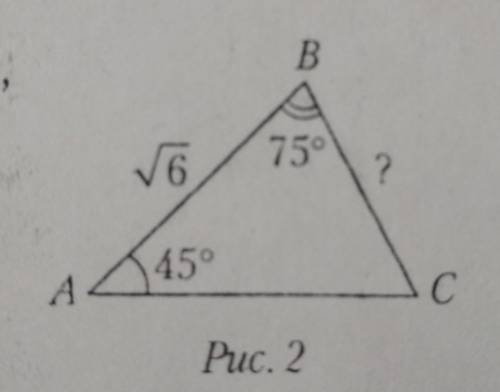
3. Если на рисунке 2 AB = √6 см,
угол A = 45°, угол B = 75°, то BC = ... :​

Для решения данной задачи мы можем использовать тригонометрию и теорему синусов.

Дано:
AB = √6 см
условие: угол A = 45°, угол B = 75°

1. Найти значение AC:
Мы можем использовать теорему синусов:
AC/sin(A) = AB/sin(B)
AC/sin(45°) = √6/sin(75°)

Для нахождения sin(75°) мы можем воспользоваться тригонометрическими формулами:
sin(75°) = sin(45° + 30°) = sin(45°)cos(30°) + cos(45°)sin(30°) = (√2/2)(√3/2) + (√2/2)(1/2) = (√6/4) + (√2/4) = (√6 + √2)/4

Подставляем полученные значения в уравнение:
AC/sin(45°) = √6/[(√6 + √2)/4]

Раскрываем скобки в знаменателе и упрощаем выражение:
AC/(√2/2) = (√6 * 4)/√6 + √2
AC = 4 * (2√6)/(√6 + √2)
AC = 8√6/(√6 + √2)

2. Найти значение BC:
Для этого можем использовать теорему синусов:
BC/sin(B) = AB/sin(A)
BC/sin(75°) = √6/sin(45°)

Мы уже нашли sin(75°) и sin(45°) ранее, поэтому подставляем значения в уравнение:
BC/(√6 + √2)/4 = √6/(√2/2)
BC = (√6 + √2)/4 * √6/(√2/2)
BC = (√6 * √6 + √2 * √6)/(4 * √2)
BC = (6 + √12)/(4 * √2)
BC = (6 + 2√3)/(4 * √2)
BC = (3 + √3)/(2√2)

Таким образом, ответ на вопрос задачи: BC = (3 + √3)/(2√2) см.