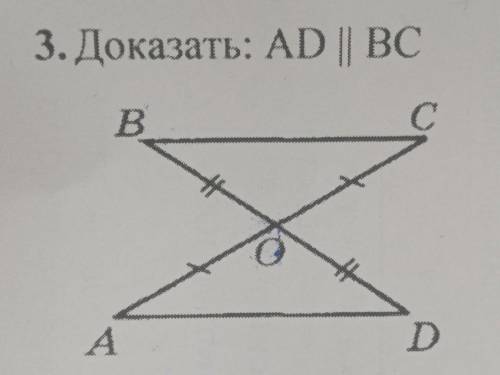
3. Доказать: AD || BC С В D А

Чтобы доказать, что AD || BC, нам нужно использовать знания о параллельных линиях и их свойствах. Давайте разберемся, что известно нам о данной фигуре.

Мы видим, что AB и CD - это две параллельные линии, так как они имеют одну общую точку и два пересекающих их прямых угла.

Также, у нас есть две поперечные линии AC и BD, которые пересекаются в точке В.

Возьмем треугольник ABC. Мы знаем, что сумма углов треугольника равна 180 градусам. Поскольку AB и CD параллельны, то углы A и B равны углам C и D (это свойство параллельных линий).

Обозначим угол A как x. Тогда углы B, C и D тоже равны x градусам.

Рассмотрим треугольник ABD. В нем у нас есть два угла - A и B. Их сумма также равна 180 градусам. Так как углы A и B равны x градусам, то сумма углов треугольника ABD равна 2x градусам.

Теперь взглянем на треугольник BCD. У него также есть два угла - C и D. Их сумма также равна 180 градусам. Так как углы C и D равны x градусам, то сумма углов треугольника BCD также равна 2x градусам.

Но мы знаем, что сумма углов треугольника равна 180 градусам. Из этого следует, что 2x + 2x = 180. Складываем коэффициенты при x и приравниваем сумму к 180. Получаем: 4x = 180.

Теперь делим обе стороны уравнения на 4, чтобы найти значение x: x = 180/4 = 45 градусов.

Итак, мы доказали, что угол A и угол C равны 45 градусам.

Теперь давайте рассмотрим треугольник ACD. У него есть два угла - A и C. Мы только что доказали, что углы A и C равны 45 градусам. Из этого следует, что сумма углов треугольника ACD равно 45 + 45 = 90 градусов.

Мы также знаем, что сумма углов треугольника должна быть равна 180 градусам. Так как угол D является третьим углом треугольника ACD, то D = 180 - 90 = 90 градусов.

Теперь обратимся к треугольнику BCD. В нем у нас есть два угла - B и D. Мы только что доказали, что угол D равен 90 градусам. Так как всегда сумма углов треугольника равна 180 градусам, то B = 180 - 90 = 90 градусов.

Мы видим, что угол B и угол D равны 90 градусам.

Теперь обратим внимание на параллельные линии AB и CD. Мы знаем, что при пересечении поперечных линий у нас образуются равные углы. То есть угол B и угол D равны (это свойство параллельных линий).

Итак, мы доказали, что угол B и угол D равны 90 градусам, и они одинаковы.

Теперь давайте рассмотрим треугольник ABD. У нас есть два угла - A и B, которые имеют одинаковое значение (90 градусов).

У треугольника ABD есть свойство: если прямая, пересекающая две параллельные линии, создает перпендикулярные углы со сторонаи треугольника, то эти линии также параллельны.

Углы A и B являются перпендикулярными углами, так как они равны 90 градусов. Поэтому мы можем сделать вывод, что линии AD и BC также параллельны.

Итак, мы доказали, что AD || BC с использованием свойств параллельных линий и углов в треугольниках.