1. Геометрия
  2. 3.Для острого угла найдите

3.Для острого угла найдите ѕin А, cos А ,tg А,
если ctg А = 2.

risimonenko risimonenko    3   14.12.2021 16:09    0

Ответы
kistina2 kistina2  04.02.2022 07:34

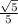
ѕin А = \frac{\sqrt{5} }{5}

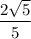
cos А = \dfrac{2\sqrt{5} }{5}

tg А = \dfrac{1}{2}

Объяснение:

1) Из основного тригонометрического тождества найдём tgα:

tg\alpha *ctg\alpha =1

tg\alpha =\dfrac{1}{ctg\alpha } =\dfrac{1}{2}

2) Так как

tg^{2} \alpha +1=\dfrac{1}{cos^{2} \alpha },

то cosα:

\dfrac{1}{cos^{2} \alpha } = 1 + tg^{2}\alpha = 1+(\dfrac{1}{2} )^{2} } = 1+\dfrac{1}{4} = \dfrac{5}{4} \\\\cos^{2} \alpha = \dfrac{4}{5} \\\\cos\alpha =\dfrac{2\sqrt{5} }{5}

3) Из основного тригонометрического тождества найдём sinα:

sin\alpha =\sqrt{1-cos^{2} \alpha } =\sqrt{1-\dfrac{4}{5} } =\sqrt{\dfrac{1}{5}} =\dfrac{\sqrt{5} }{5}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
BAMBELBI013 BAMBELBI013  26.01.2021 16:00
Найти площадь параллелограмм​...
zziimmbboo zziimmbboo  26.01.2021 16:01
Решите умоляю надо (на фото)...
мария21112006 мария21112006  30.08.2019 11:50
Решите. в треугольнике abc известно, что угол c = 90 градусов, угол b = 60 градусов....
botanurmanova botanurmanova  30.08.2019 11:50
Точки a и b лежат по разные стороны от прямой mk докажите ,что треугольник amc=bkm...
dasha20015678 dasha20015678  30.08.2019 11:50
Впрямоугольном треугольнике abc с прямым углом c проведены биссектрисы a a1 и b b1, пересекающиеся в точке i.найдите угол a1ib1...
Ааапллортдопсмтдд Ааапллортдопсмтдд  08.10.2019 03:01
На чиртите отрезок ави разделить его в отношении 5: 4​...
Føxŷ12 Føxŷ12  08.10.2019 03:01
Диагональ куба равна 27.найти площадь поверхности куба​...
sobchuk555 sobchuk555  08.10.2019 03:01
Авс үшбұрышында ad-биссектрисасы,с бұрышы 30 градус,bad бұрышы 22 градус.adb бұрышын табыңдар....
Ashhhhhhhhhhhhh Ashhhhhhhhhhhhh  08.10.2019 03:01
Сочинение рассуждение на любую тему (100 слов минимум)...
MrLeysanHD MrLeysanHD  10.03.2021 16:57
Ребят ! Контрольная работа по геометрии Кусок средней линии трапеции Основания трапеции равны 8 и 22. Найдите больший из отрезков, на которые среднюю линию делит...

Популярные вопросы