2. В треугольнике АВС (рис. 1) BC = 6, a=30°. Используя формулу a/sinA=2R. Найдите радиус окружности, описанной около треугольника АВС: a) 3; б) 4; b) 6; г) 2,5.
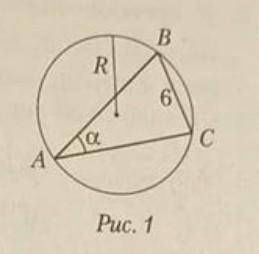
Другие вопросы по теме Геометрия
Популярные вопросы
- Представте в виде десятичной дроби числа три целых одна вторая номер 1588...
1 - С. 1.найдите значение выражения. 6/7 *(0,76)-2,74*6/7. 2. выполните действия. (36,67+2,9*(-3,8)):...
1 - Ионное уравнение, сделать! nacl+agno3...
2 - На клумбы розцвыли 15 троянд скыльки можна отримати букутыв якщо в кожен брати по...
3 - Отметь слово с открытым слогом a)game b)pen c)pin d)myth...
2 - Вычислите объем кислорода (н.у) необходимого для сгорания 2 л пропана...
3 - На приилавке лежало 27 красных и 34 зеленые тетради. когда положили еще несколько...
2 - Составь уровнение по тексту и реши его: мама купила 3кг рыбы по 35р. за килограмм...
2 - Распределите формулы по классам и назовите их. а)ch3-ch3. б)ch2=ch2 b)ch3oh г)hcooh...
3 - Поднялась большая тёмная туча.хлынул проливной дождь.после дождя в лесу сильно пахнет...
2
На рисунке 1 видно, что треугольник АВС имеет сторону BC длиной 6, а противолежащий угол A равен 30°. Нам нужно найти радиус R описанной окружности при разных значениях длины стороны a.
a) Если a = 3, подставляем значения в формулу:
3/sin30° = 2R
3/(1/2) = 2R
6 = 2R
Делим обе части уравнения на 2:
3 = R
Таким образом, радиус описанной окружности при a = 3 равен 3.
б) Если a = 4:
4/sin30° = 2R
4/(1/2) = 2R
8 = 2R
4 = R
Таким образом, радиус описанной окружности при a = 4 равен 4.
в) Если a = 6:
6/sin30° = 2R
6/(1/2) = 2R
12 = 2R
6 = R
Таким образом, радиус описанной окружности при a = 6 равен 6.
г) Если a = 2.5:
2.5/(sin30°) = 2R
2.5/(1/2) = 2R
5 = 2R
5/2 = R
Таким образом, радиус описанной окружности при a = 2.5 равен 2.5/2 = 1.25.
Итак, ответы на задачу:
а) Радиус описанной окружности при a = 3 равен 3.
б) Радиус описанной окружности при a = 4 равен 4.
в) Радиус описанной окружности при a = 6 равен 6.
г) Радиус описанной окружности при a = 2.5 равен 1.25.