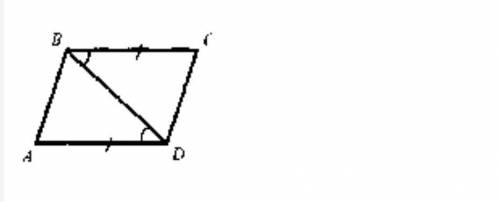
№2 Дано: ВС=АD, ∟СВD= ∟ВDА
Доказать: АВD= DВС.
Найти ∟ВDС, если ∟АВD=66 градусам
​

Для доказательства утверждения "АВD= DВС" нужно использовать определение равенства углов: если две пары углов равны, то их третьи углы тоже равны. Исходя из данных, у нас есть следующие равенства: 1. ВС=АD (дано) 2. ∟СВD= ∟ВDА (дано) 3. ∟АВD=66 градусов (дано) По условию требуется доказать, что АВD= DВС. Для этого нужно использовать определение равенства углов. Докажем равенство АВD= DВС пошагово: 1. Добавим отрезок ВЕ к треугольнику ВСD, чтобы получить новый треугольник ВЕD. 2. Так как ВС=АD (дано), то вершины С и D являются серединами отрезка ВЕ. 3. Поэтому отрезок СD является медианой треугольника ВЕD. 4. Так как медиана в треугольнике делит противолежащий ей угол пополам, то получаем, что ∟ВDС= ∟ВСD. 5. По условию ∟СВD= ∟ВDА (дано). 6. Из равенств ∟ВDС= ∟ВСD и ∟СВD= ∟ВDА следует, что ∟ВDС= ∟ВDА. Таким образом, мы доказали, что АВD= DВС. Теперь найдем ∟ВDС. Из доказанного равенства АВD= DВС следует, что если ∟АВD=66 градусов, то ∟ВDС тоже равно 66 градусов. Ответ: АВD= DВС и ∟ВDС=66 градусов.