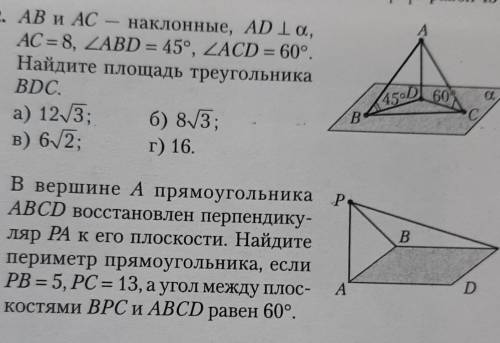
2. AB и AC - наклонные, AD 1 а, AC = 8, ZABD = 45°. ZACD = 60°.
Найдите площадь треугольника
BDC.
3. В вершине А прямоугольника
ABCD восстановлен перпендику-
ляр РA к его плоскости. Найдите
периметр прямоугольника, если
PB = 5, PC = 13, а угол между плос-
Костями BPC и ABCD равен 60°.​

Ответ в12 ²
Найдена плошадь треугольник

Для решения этой задачи нам понадобятся знания о геометрических свойствах треугольников и прямоугольников.

1. Найдем площадь треугольника BDC. Для этого нам понадобятся длины сторон треугольника и значение угла между ними.

Из условия задачи мы знаем, что AB и AC - наклонные, AD = 1 см, AC = 8 см, ZABD = 45° и ZACD = 60°.

Сначала найдем длину стороны BD. Для этого воспользуемся теоремой синусов в треугольнике ABD:

sin(ZABD) / AD = sin(ZBAD) / BD

Подставляем известные значения:

sin(45°) / 1 = sin(ZBAD) / BD

Так как sin(45°) = √2 / 2, получим:

(√2 / 2) = sin(ZBAD) / BD

Упрощаем:

√2 = (BD * sin(ZBAD)) / 2

Умножаем обе части уравнения на 2:

2√2 = BD * sin(ZBAD)

Таким же образом, используем теорему синусов в треугольнике ACD:

sin(ZACD) / AD = sin(ZACD) / CD

sin(60°) / 1 = sin(ZACD) / CD

Так как sin(60°) = √3 / 2, получим:

(√3 / 2) = sin(ZACD) / CD

Упрощаем:

√3 = (CD * sin(ZACD)) / 2

Умножаем обе части уравнения на 2:

2√3 = CD * sin(ZACD)

Теперь имея значения BD и CD, можно воспользоваться формулой для площади треугольника:

Площадь треугольника BDC = (1/2) * BD * CD * sin(ZBDC)

Подставляем известные значения:

Площадь треугольника BDC = (1/2) * (√2) * (√3) * sin(ZBDC)

Умножаем числител именатель на корень из 6:

Площадь треугольника BDC = (1/2) * (√2 * √3) * √6 * sin(ZBDC)

Площадь треугольника BDC = (1/2) * √6 * sin(ZBDC)

Таким образом, площадь треугольника BDC равна (1/2) * √6 * sin(ZBDC).

2. Теперь рассмотрим вторую задачу. Нам необходимо найти периметр прямоугольника ABCD.

Из условия задачи мы знаем, что PB = 5 см, PC = 13 см и угол между плоскостями BPC и ABCD равен 60°.

Из этого угла мы можем определить угол между сторонами PB и PC. Так как сумма углов треугольника равна 180°, то угол BPC равен 180° - 60° = 120°.

Теперь мы можем воспользоваться теоремой косинусов, чтобы найти длину стороны BC:

BC² = PB² + PC² - 2 * PB * PC * cos(ZBPC)

Подставляем известные значения:

BC² = 5² + 13² - 2 * 5 * 13 * cos(120°)

BC² = 25 + 169 - 130 * cos(120°)

Так как cos(120°) = -1/2, получим:

BC² = 25 + 169 + 130/2

BC² = 25 + 169 + 65

BC² = 259

BC = √259

Теперь мы можем найти периметр прямоугольника ABCD:

Периметр ABCD = 2 * (AB + BC)

AB = BC, так как прямоугольник ABCD является прямоугольником

Периметр ABCD = 2 * (BC + BC)

Периметр ABCD = 4 * BC

Периметр ABCD = 4 * √259.

Таким образом, периметр прямоугольника ABCD равен 4 * √259.