1704. в треугол. авс ав=вс=ас=54√3. найдите высоту вн 1706 в треугол. авс ав=вс-ас=46√3. найдите высоту сн 1711 в треугол. авс ас=вс=54,угол с=30 гр.найдите высоту ан

Ответы

nastusya0307 15.06.2020 02:42

1704.

Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=27√3. Основание AC. Далее рассмотрим треугольник ABH - прямоугольный. По теореме Пифагора находим BH:

$BH=\sqrt{(54\sqrt{3})^2 - (27\sqrt{3})^2}= \sqrt{8748-2187}=\sqrt{6561}=81$

BH=81

1706.

Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=23√3. Основание AB. Далее рассмотрим треугольник ACH - прямоугольный. По теореме Пифагора находим CH:

$CH=\sqrt{(46\sqrt{3})^2 - (23\sqrt{3})^2 }=\sqrt{6348-1587}=\sqrt{4761}=69$

CH=69

1711.

Так как треугольник ABC - равнобедренный, то угол B и угол C равны по 30 градусов.
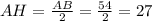
Рассмотрим один из двух треугольников ABH - прямоугольный.
По свойству мы знаем, что катет лежащий против угла в 30 градусов равен половине гипотенузы, отсюда следует, что:
$AH=\frac{AB}{2}=\frac{54}{2}=27$