17. Основания трапеции равны 18 и 7, одна из боковых сторон равна 12, а косинус угла между ней и одним из оснований равен

Найдите пло-

щадь трапеции.

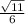
$\frac{ \sqrt{11} }{6}$

Ответы

SvetaX16X 03.05.2022 09:08

щадь насрал на стол щадь насрал на стол

ПОКАЗАТЬ ОТВЕТЫ

Ekaterina200130 08.01.2024 19:57

Добрый день! Давайте решим эту задачу.

Данная задача связана с трапецией, поэтому давайте вспомним, что такое трапеция. Трапеция - это четырехугольник, у которого две противоположные стороны параллельны, и две другие стороны непараллельны.

В данной задаче нам даны два основания трапеции, длины которых равны 18 и 7, и одна из боковых сторон, длина которой равна 12.

Для решения задачи нам также дан косинус угла между этой боковой стороной и одним из оснований, его значение равно $\frac{ \sqrt{11} }{6}$ .

Для начала, нам потребуется найти величину этого угла. Для этого вспомним, что косинус угла - это отношение прилежащего катета к гипотенузе прямоугольного треугольника.

Так как у нас уже известны длины сторон в трапеции, можно построить прямоугольный треугольник, у которого стороны соответствуют основанию трапеции, боковой стороне и высоте трапеции.

Для этого воспользуемся теоремой Пифагора: сумма квадратов катетов равна квадрату гипотенузы.

В нашем случае:
Одно основание трапеции равно 7,
одна боковая сторона - 12,
а второе основание будет являться гипотенузой.

По теореме Пифагора: 12^2 = 7^2 + x^2, где x - длина второй основания трапеции.

Решим это уравнение:
144 = 49 + x^2,
x^2 = 144 - 49,
x^2 = 95,
x = sqrt(95).

Таким образом, длина второго основания трапеции равна sqrt(95).

Теперь давайте найдем площадь трапеции. Формула для нахождения площади трапеции: S = (a + b) * h / 2, где a и b - основания трапеции, h - высота трапеции.

У нас первое основание равно 18, второе основание - sqrt(95), но нам не дана высота трапеции.

Однако, чтобы найти высоту трапеции, нам поможет данное значение косинуса угла между боковой стороной и одним из оснований. Косинус угла - это отношение прилежащего катета к гипотенузе прямоугольного треугольника.

Мы уже нашли длины сторон прямоугольного треугольника в процессе решения предыдущей части задачи: прилежащий катет - 7, гипотенуза - sqrt(95).

Тогда cos(угла) = 7 / sqrt(95).

Данное значение косинуса угла равно $\frac{ \sqrt{11} }{6}$ , поэтому можем записать следующее уравнение:

7 / sqrt(95) = $\frac{ \sqrt{11} }{6}$ .

Для упрощения уравнения, помним, что деление на дробь эквивалентно умножению на обратную дробь. Тогда:

7 / sqrt(95) = $\frac{ \sqrt{11} }{6}$ ,
sqrt(95) = 7 * 6 / sqrt(11),
sqrt(95) = 42 / sqrt(11).

Для упрощения подходящих объемов, умножаем выражение на дробь сопряженное к корню:

sqrt(95) * sqrt(11) = 42 / sqrt(11) * sqrt(11),
sqrt(1045) = 42.

Теперь мы можем найти высоту трапеции, используя теорему Пифагора. Зная значения катета и гипотенузы, мы можем решить следующее уравнение:

18^2 = h^2 + 42^2,
324 = h^2 + 1764,
h^2 = 1440,
h = sqrt(1440).

Таким образом, высота трапеции равна sqrt(1440).

Теперь мы можем продолжить нахождение площади трапеции, используя формулу S = (a + b) * h / 2:

S = (18 + sqrt(95)) * sqrt(1440) / 2.
S = (18 + sqrt(95)) * sqrt(1440) / 2.
S = (18 + sqrt(95)) * 12 * sqrt(10) / 2.
S = (18 + sqrt(95)) * 6 * sqrt(10).

Таким образом, площадь трапеции равна (18 + sqrt(95)) * 6 * sqrt(10).

Это окончательный ответ на задачу.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия