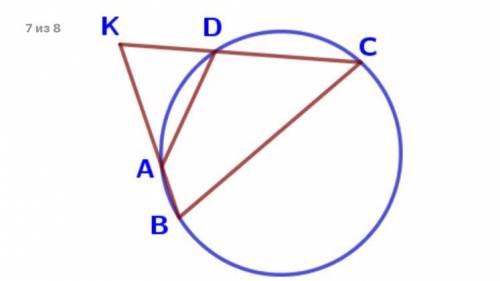
17. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=14, DK=8, BC=21. Найдите AD.

Для решения данной задачи мы можем использовать свойства вписанных углов и свойств подобных треугольников.

1. Из свойства вписанных углов мы знаем, что угол ABC равен углу ADC. Отсюда следует, что треугольники ABC и ADC подобны, так как у них равны два угла.

2. Отношение длин сторон подобных треугольников равно. Поэтому можно записать:

AB/AD = BC/CD

Заменяем известные значения:
AB/AD = 21/8

3. Перемножаем числитель и знаменатель пропорции:

AB * CD = AD * BC

Заменяем известные значения:
14 * CD = AD * 21

4. Разделим обе части уравнения на 14:

CD = (AD * 21) / 14

5. Сократим дробь:

CD = (3/2) * AD

6. Проанализируем треугольник BCD. Известно, что AD + CD = BC. Подставляем значения:

AD + (3/2) * AD = 21

Упрощаем уравнение:
(5/2) * AD = 21

7. Разделим обе части уравнения на (5/2):

AD = 21 / (5/2)

Упростим дробь, разделив числитель и знаменатель на 7:
AD = 6 / (5/2)

8. Домножим дробь на обратное значение делителя:

AD = 6 * (2/5)

Умножаем числитель и знаменатель:
AD = 12/5

Таким образом, длина отрезка AD равна 12/5 (или 2.4 в десятичной записи).