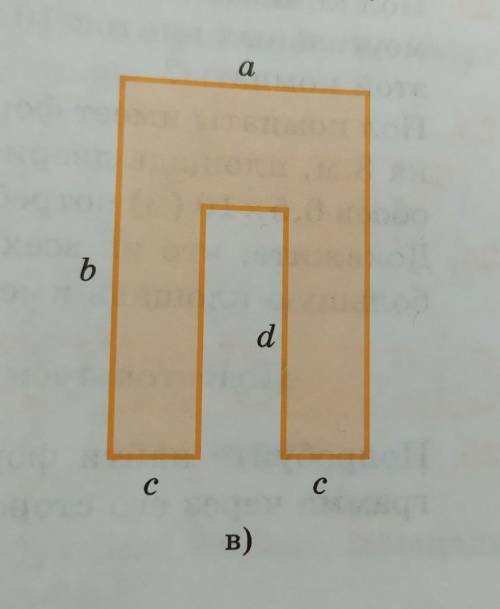
16. Найдите площади фигур, изображенных на рисунке 19.13.
с решением

Добрый день! Рад, что вы обратились за помощью. Давайте разберемся с этим вопросом.

На рисунке 19.13 изображены две фигуры - треугольник ABC и прямоугольник DEFG. Нашей задачей является нахождение площадей этих фигур.

1. Начнем с треугольника ABC. Заметим, что дан треугольник прямоугольный, так как угол BAC обозначен прямым углом. Для нахождения площади прямоугольного треугольника воспользуемся формулой: Площадь = (основание * высота) / 2.

Основание треугольника - это сторона, на которую опирается треугольник, в данном случае это сторона BC. Высота треугольника - это расстояние от вершины треугольника, перпендикулярно основанию. Для нахождения высоты обычно используют перпендикуляр из вершины к основанию, но на рисунке он не дан. Воспользуемся другим методом нахождения высоты.

Заметим, что сторона DE противолежит углу BAC, значит, она может быть использована в качестве высоты треугольника. Теперь посчитаем основание треугольника - BC. По рисунку видно, что BC = 10 см. Высота треугольника - DE = 6 см.

Подставляем все значения в формулу: Площадь = (10 * 6) / 2 = 30 / 2 = 15 см².

Таким образом, площадь треугольника ABC равна 15 квадратным сантиметрам.

2. Теперь перейдем к прямоугольнику DEFG. Для нахождения площади прямоугольника используется формула: Площадь = длина * ширина.

На рисунке даны длина и ширина прямоугольника: DE = 6 см и DG = 10 см.

Подставляем значения в формулу: Площадь = 6 * 10 = 60 см².

Таким образом, площадь прямоугольника DEFG равна 60 квадратным сантиметрам.

Таким образом, мы нашли площади обеих фигур, изображенных на рисунке 19.13. Площадь треугольника ABC равна 15 квадратным сантиметрам, а площадь прямоугольника DEFG равна 60 квадратным сантиметрам.

Если у вас возникнут еще вопросы или понадобится дополнительное пояснение, не стесняйтесь спрашивать. Я всегда готов помочь.