145. На рис. 171 CE = ЕК, PM=KE Доказать, что
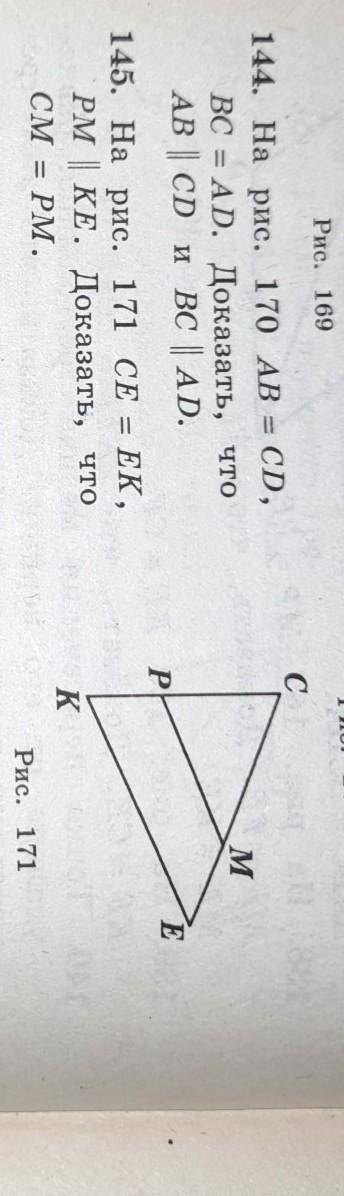
Другие вопросы по теме Геометрия
Популярные вопросы
- усно перемалювати ілюстрацію яка не точно відповідає зображеному...
2 - решить Уравнение окружности. Урок 2...
1 - Синонимы Ұзын – [1] Кісі – [1] Көп – [1] Салқын – [1] Жоғарлататын...
3 - Клітинну стінку мають клітини:А бактерійБ рослинВ грибівГ усі відповіді...
1 - ДОМАШНЕЕ ЗАДАНИЕ 9Реши задачу.К космодрому ведет шоссе. Надо отре-монтировать...
1 - напишите рж про день рождение))...
3 - 578:3=? Сколько? Надо здать 28.04.21!...
2 - Астана əсем кала такырыбына əңгіме құра...
2 - Напишите рецензию на работу своего одноклассника...
2 - Дайте письмову відповідь на питання Які проблеми прорушує В. Стус...
2
Объяснение:
Рассмотрим треугольники CPM и СEK
Угол С у них общий, угол CMP = углу CEK ( как соответственные углы при параллельных прямых PM и KE, следовательно треугольники CPM и CKE - подобные.
Если в треугольнике CEK CE = EK, то и в треугольнике CMP CM = MP, так как треугольники подобны
В изначальном условии дано, что CE = EK, PM = KE. Мы должны доказать, что PM = EC.
Для начала, обратим внимание на то, что треугольник СЕК является равнобедренным, так как его боковые стороны CE и EK равны. Из этого следует, что угол СЕК также равен углу СКЕ.
Теперь обратим внимание на треугольник РМЕ. Из условия PM = KE и того, что CE = EK, получаем, что PM = CE.
Теперь взглянем на треугольник СЕМ. Мы знаем, что угол СЕМ равен углу СКЕ (так как СЕК - равнобедренный треугольник). Также, угол ПМЕ равен углу МЕК (как вертикальные углы).
Теперь обратим внимание на треугольник СМЕ. У него угол МЕС равен углу СЕМ (как вертикальные углы).
Таким образом, мы получаем, что треугольник СЕМ является равнобедренным, так как у него боковая сторона СМ равна боковой стороне МЕ и углы у основания ГМЕ равны.
Следовательно, искомое соотношение PM = EC также верно, так как мы только-что доказали равнобедренность треугольника СЕМ.
Таким образом, мы доказали, что PM = EC.