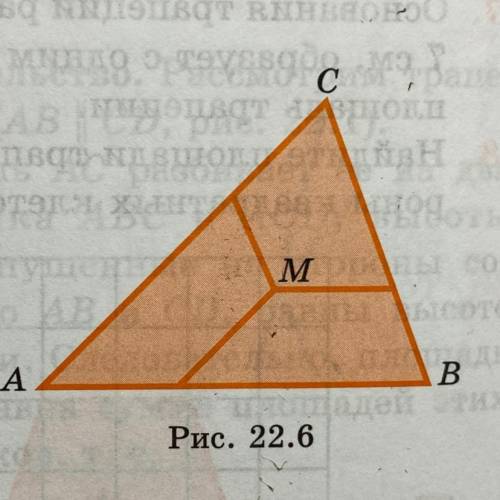
14. В треугольнике ABC через точку М пересечения его медиан про- ведены отрезки, параллельные сторонам треугольника (рис. 22.6).
Докажите, что образовавшиеся при этом три трапеции равновелики.
P.S. Можете подробно расписать с объяснением
Другие вопросы по теме Геометрия
Популярные вопросы
- Стих с большим количеством имен прилагательных...
1 - Решительно : расстояние между 129 км.скорость 1 велосипедиста 12км/ч,а...
3 - Назовите климатический пояс по краткому описанию: в данном пояса зимой...
3 - Запись 5н2 обозначает а) 5 атомов водорода; б) 10 атомов водорода; в)...
1 - Твір-оповідання про випадок із життя...
1 - Смысл названия рассказа тихое утро!...
3 - Записать по 3 слова имени существительных, оканчивающиеся на: ч- чь- ж-...
3 - Нужно написать несколько загадок про профессии на языке с переводом...
1 - Надо завтра 50 найти точек максимума y= -2 sin (x+pi/4)...
3 - Краткий реферат нужно написать можно из интернета на казахском языке про...
3
Для начала, давайте рассмотрим свойство медиан треугольника. Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае, отрезки AM, BM и CM являются медианами треугольника ABC.
Свойство медианы, которое нам поможет в доказательстве, заключается в том, что медианы делятся точкой пересечения на две равные части. То есть, отрезок AM делит сторону BC пополам, отрезок BM делит сторону AC пополам, и отрезок CM делит сторону AB пополам.
Теперь, давайте рассмотрим три трапеции, образовавшиеся при проведении отрезков, параллельных сторонам треугольника. Обозначим эти трапеции как PQR, STU и VWX (см. рисунок).
Так как отрезки PQR, STU и VWX параллельны соответствующим сторонам треугольника, то у них есть одинаковые основания:
1) Основание трапеции PQR - сторона AB треугольника ABC
2) Основание трапеции STU - сторона BC треугольника ABC
3) Основание трапеции VWX - сторона AC треугольника ABC
Также, мы знаем, что высоты трапеций PQR, STU и VWX равны между собой, так как они проведены из точки M - пересечения медиан треугольника. Обозначим высоты этих трапеций как h1, h2 и h3 соответственно.
Наша цель - доказать, что площади этих трапеций равны. Для этого нам нужно доказать, что произведение основания на высоту для каждой трапеции одинаково.
Для трапеции PQR:
Площадь трапеции PQR = (AB + PQ)*h1
Обратите внимание, что AB + PQ = AM + MQ. Но по свойству медианы, AM = MQ, поэтому AB + PQ = 2*AM = BC.
Таким образом, площадь трапеции PQR = BC*h1.
Для трапеции STU:
Площадь трапеции STU = (BC + ST)*h2
Аналогично, BC + ST = BM + MT = AM = AC.
Поэтому, площадь трапеции STU = AC*h2.
Для трапеции VWX:
Площадь трапеции VWX = (AC + VW)*h3
Аналогично, AC + VW = CM + MV = BM = AB.
Поэтому, площадь трапеции VWX = AB*h3.
Теперь, чтобы доказать, что площади трапеций PQR, STU и VWX равны, нам нужно показать, что BC*h1 = AC*h2 = AB*h3.
Мы знаем, что AM делит BC пополам, поэтому BC = 2*AM. Также, по свойству медианы, AM = MQ, и MQ делит AC пополам, поэтому AC = 2*MQ = 2*h2. Наконец, по свойству медианы, AM = MQ = MP, и MP делит AB пополам, поэтому AB = 2*MP = 2*h3.
Следовательно, BC*h1 = 2*AM*h1 = 2*(AM*h1) = 2*(MQ*h1) = 2*(MQ*h2) = 2*AC = AC*h2 = 2*MQ*h2 = 2*(MQ*h2) = 2*(MQ*h3) = AB*h3.
Таким образом, мы доказали, что площади трапеций PQR, STU и VWX равны.
Это доказывает, что три трапеции, образовавшиеся при проведении отрезков через точку M пересечения медиан треугольника, равновелики.