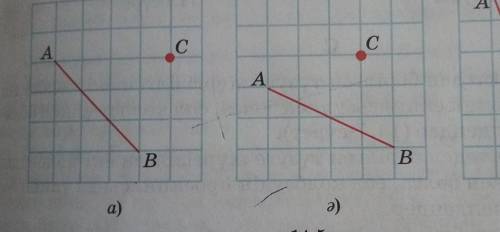
14.5. Торкөзді қағазда, 14.5-суретте көрсетілгендей, нүктелер мен түзулерді кескіндеңдер. С нүктесінен АВ түзуіне CD перпенди-
кулярын түсіріңдер.
​

Хорошо, я готов ответить на ваш вопрос о задаче 14.5.

Так как на рисунке дано только две точки, A и B, и их координаты не указаны, нам придется использовать геометрический подход для решения задачи.

Предположим, что координаты точки A - (x1, y1), а координаты точки B - (x2, y2). Тогда, чтобы найти координаты точки C, нам необходимо использовать уравнение серединного перпендикуляра.

Серединный перпендикуляр - это прямая, проходящая через середину отрезка AB и перпендикулярная ему.

1. Найдите середину отрезка AB.
Середина отрезка AB имеет координаты:
x_середина = (x1 + x2) / 2
y_середина = (y1 + y2) / 2

2. Найдите угловой коэффициент прямой AB.
Угловой коэффициент прямой AB можно найти, используя формулу:
k_AB = (y2 - y1) / (x2 - x1)

3. Найдите угловой коэффициент перпендикуляра к AB.
Угловой коэффициент перпендикуляра равен отрицанию обратного углового коэффициента AB:
k_перпендикуляр = -1 / k_AB

4. Используя полученный угловой коэффициент перпендикуляра, найдите уравнение прямой, проходящей через точку C.
Уравнение прямой с угловым коэффициентом k_перпендикуляр, проходящей через точку C(x_середина, y_середина), имеет вид:
y - y_середина = k_перпендикуляр * (x - x_середина)

5. Решите уравнение прямой для нахождения координат точки C.
Подставьте известные значения x и y в уравнение прямой:
y_середина = k_перпендикуляр * (x - x_середина) + y_середина
Решите это уравнение относительно x, чтобы найти x-координату точки C. Затем подставьте найденное значение x в уравнение прямой, чтобы найти y-координату.

Это пошаговое решение задачи 14.5 на нахождение координат точки C.