100б
1) Диагонали равнобокой трапеции перпендикулярные. Найдите радиус окружности, описанной около трапеции, если ее боковая сторона равна 7√2 см.
2) Площадь равнобедренного треугольника равна 192см2, а радиус вписанной окружности – 6 см. Найдите стороны треугольника, если его основание на 4 см больше боковой стороны.
Нужно подробное решение!

На сколько я понял требуется решить только первую задачу.

Дана трапеция ABCD, AB=CD=7√2 см; AC⊥BD.

Найти радиус описанной около ABCD.

Пусть AC∩BD=F и пусть ∠FAB=α.

Вокруг равнобедренной трапеции всегда можно описать окружность!

ΔABD=ΔDCA по двум сторонам и углу между ними (AB=DC; AD - общая; ∠BAD=∠CDA), поэтому ∠ADB=∠DAC, как углы лежащий напротив равных сторон в равных треугольниках.

В ΔAFD:

∠AFD=90°; ∠FAD=∠FDA=(180°-∠AFD):2=90°:2=45°. Таким образом ΔAFD - равнобедренный прямоугольны, AF=DF.

В прямоугольном ΔAFB:

AF=AB·cosα=7√2·cosα см

BF=AB·sinα=7√2·sinα см

В ΔABD:

BD=BF+FD=BF+AF=7√2·(sinα+cosα) см

∠BAD=α+45°

Вокруг ΔABD описана таже окружность, что и вокруг трапеции.

По теореме синусов: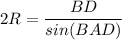 , где R - радиус описанной.

ответ: 7 см.