100 ! с рисунком ! основою піраміди є прямокутний трикутник з катетом а і прилеглим до нього гострим кутом α. дві бічні грані, що містять катети цього трикутника перпендикулярні до площини основи, а третя – нахилена до неї під кутом β. знайдіть об'єм піраміди.
Другие вопросы по теме Геометрия
Популярные вопросы
- Выбери три верные утверждения. (Запиши в ответе цифры в порядке их...
2 - Массивы1. В программе используется одномерный целочисленный массив...
3 - По мнению учёных первый пилотируемый корабль отправится на марсианский...
1 - При каких значениях с двучлен 10x — 4 принимает отрицательные значения?...
2 - 1. Привидите естественных экосистем - 2. Какую роль играют в экосистеме...
1 - Определите длину волны, на которой работает передатчики скусственного...
1 - Rewrite the sentences in the present simple passive1 Millions of...
1 - Твір Дракони вперед скласти анотацію с прислівниками ...
3 - по повести Дубровского; Почему приезд Владимира не его отца? Чем...
2 - Hное давлездесь космонавтказались теUе пит1. В космосе в условиях...
3
Основанием пирамиды является прямоугольный треугольник с катетом а и прилегающим к нему острым углом α. Две боковые грани, содержащие катеты этого треугольника, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объем пирамиды.
========
Пусть в данной пирамиде АВС - основание. угол С=90°, ВС=а, ∠АВС=α, MC⊥(ABC) – высота пирамиды. Угол между АВС и АМВ=β.
Формула объёма пирамиды V=S•H:3
Угол МНС - линейный угол угла между плоскостями основания и грани АМВ и равен углу между перпендикулярами, проведенными к одной точке на АВ.
МН - наклонная, перпендикулярна АВ, СН - её проекция на АВС.⇒ По т. о 3-х перпендикулярах угол СНВ=90°, а СН - высота ∆ АВС
S=a•b•sinα:2 ⇒
S(АВС)=AB•BC•sinα:2
АВ=ВС:cosα=a:cosα
S(АВС)=(a:cosα)•a•sinα:2=a²sinα:2cosα
H=MC=CH•tgβ
CH=BC•sinα=a•sinα
H=a•sinα•tgβ
V=(a²•sinα:2cosα)•a•sinα•tgβ:3⇒
ответ: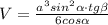
: