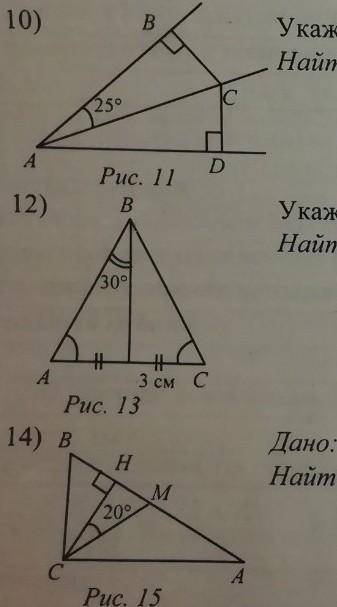
10) Укажите равные треугольники. Найти: угол BCD. 12) Укажите равные треугольники. Найти: АВ
14) Дано: СМ - медиана. Найти: угол А, угол В. ​

10) Чтобы понять, какие треугольники равные, нам нужно сравнить их стороны и углы. Равные треугольники имеют все равные стороны и равные углы. В данной задаче, нам необходимо найти угол BCD.

12) Опять же, чтобы найти равные треугольники, мы должны сравнить их стороны и углы. Мы также должны решить задачу, указанную в вопросе "найти АВ".

14) В данной задаче, дано, что СМ - медиана. Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Нам нужно найти угол А и угол В.

Для решения этих задач, нам необходимо использовать свойства треугольников и применять различные формулы и теоремы.

Опишу решение каждой задачи по порядку:

10) Чтобы определить равные треугольники, мы сравним их стороны и углы. На изображении мы видим, что сторона CD и сторона BD в обоих треугольниках равны. Также, углы BCD и BDC оба равны 90 градусов. Поэтому, треугольники BCD и BDC равны.

Теперь, чтобы найти угол BCD, мы можем использовать свойство суммы углов треугольника, где сумма углов треугольника всегда равна 180 градусов. Угол BDC равен 90 градусов, поэтому, угол BCD равен 180 - 90 = 90 градусов.

12) Для поиска равных треугольников, нам нужно сравнивать их стороны и углы. В данном случае, сторона AB и сторона AC в обоих треугольниках равны. Углы BAC и BCA также равны. Поэтому, треугольники ABC и ACB равны.

Чтобы найти АВ, нам нужно решить задачу. Однако, нам не даны другие значения или углы, поэтому точный ответ не может быть найден только с использованием предоставленных данных.

14) В данной задаче, мы знаем, что CM является медианой треугольника. Медиана делит противоположную сторону на две равные части. То есть, либо угол AMB, либо угол BMC, должны быть прямыми углами (равны 90 градусам).

Но вопрос требует найти угол А и угол В. Нам не даны другие углы или значения сторон, поэтому точного ответа не возможно определить только с использованием предоставленных данных.

Все эти задачи требуют более подробной информации или дополнительных условий, чтобы дать точные ответы. Недостаточно данных, чтобы определить значения углов или размеров сторон треугольников. Необходимо иметь более подробную информацию, чтобы решить эти задачи.