1) В параллелограмме ABCD точка M – середина BC, а точка K – середина AD. Найдите отношение длин отрезков, на которые прямые AM и CK разделили диагональ BD.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.Федерация – это 1) родина 2) союз, объединение 3) отечество 4) содружество 2...
1 - ..не понимаю.тема:расчеты пути,времени и скорости движения тела...
2 - Как делать по музыке делать это сыграй песни на фортепиано со счётом вслух. Считай...
2 - Распределите события в хронологическом порядке...
2 - Характеристика колониальной политики португалии .....
1 - И.С.Никитин .Стихотворения Русь , Сибирь! Напишешь это слово... . М.Ю.Лермонтов....
2 - Найдите координаты вершины с параллелограмма ABCD, если А (-3; 3), B (-1; 4),...
1 - Назовите виды равновесия ,изображения на рисунке это...
2 - Чи може точка А лежати між точками В і С якщо AB 3.6 см, BC 8.3 см AC 4.7 відповідъ...
3 - Ә.Қайдардың 《Халық даналығы》кітабынан отбасындағы тәрбие қатысты бес мақал-мәтелді...
3
В параллелограмме ABCD точка M – середина BC, а точка K – середина AD. Найдите отношение длин отрезков, на которые прямые AM и CK разделили диагональ BD.
Объяснение:
1) Т.к. ABCD-параллелограмм, то ВС=АD ⇒ MC=AK.
Тогда АМСК- параллелограмма по признаку о двух равных и параллельных сторонах (MC=AK, MC ║AK) ⇒ АМ║КС.
2)По т. Фалеса для ∠СВD получаем ВР=РН.
По т. Фалеса для ∠ADB получаем РН=НD.
Тогда ВР=РН=НD.
Поэтому отношение длин отрезков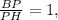
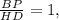
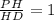 .
.