1. в параллелограмме abcd ав(вектор) = а (вектор), ad(вектор) = b ( вектор). выразить векторы ас и bd через векторы a, b. 2. в прямоугольнике abcd стороны равны 9 см и 40 см. найти /db - da + bc/ (вектора)

Ответы

ayer1 06.06.2020 23:34

1. Параллелограмм ABCD.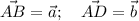 $\vec {AB}=\vec a;~~~\vec {AD} = \vec b$

Сложение векторов по правилу параллелограмма :

$\boldsymbol{\vec {AC} = \vec a + \vec b}$

Сложение векторов по правилу треугольника :

$\boldsymbol{\vec {BD}} = \vec {BA}+\vec{AD}=-\vec a + \vec b=\boldsymbol{\vec b - \vec a}$

=============================================

2. Прямоугольник ABCD, AB=CD=9 см; AD=BC=40 см

$|\vec {DB} - \vec {DA} + \vec {BC}|=|\vec {AB} + \vec {BC}|=|\vec {AC}|$

Длина вектора АС вычисляется, как длина гипотенузы АС в прямоугольном треугольнике ABC по теореме Пифагора :

$\boldsymbol{|\vec {AC}|}=\sqrt{AB^2+BC^2}=\sqrt{9^2+40^2}=\sqrt{1681} =\boldsymbol{41}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

anoNim13414 09.12.2020 08:04

б) задание очень надо с рисунком ...

romaroma6 09.12.2020 08:05

Fansik34324 05.05.2021 07:43

можно 7 и если не затруднит 8...

denzozp08hc1 05.05.2021 07:43

никита3501 29.04.2020 17:16

WowRenka 29.04.2020 17:16

artemmavericksmesrri 29.04.2020 17:16

ENOT234u 29.04.2020 17:16

Ali0429 13.07.2019 15:20

Втреугольнике abc угол c прямой ,bc=12,tga=1,5 ,найдите ac...

linakirilinaa 10.11.2019 18:46