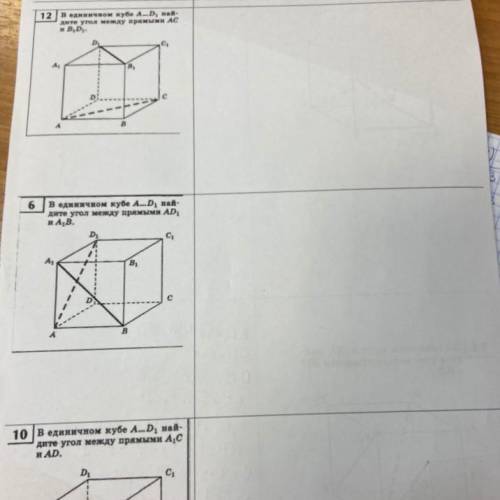
1) В единичном кубе A_D1 найдите угол, между прямыми AC и B1D1 2) найдите угол между AD1 и A1B
3) найдите угол между A1C и AD

Объяснение:

Решаем с векторов.

ab1 = aa1 + a1b1

bc1 = bb1 + b1c1 = aa1 + b1c1

(ab1, bc1) = ((aa1 + a1b1),(aa1 + b1c1)) =

aa1 * aa1 + aa1 * b1c1 + a1b1*aa1 + b1c1*a1b1 =

1 + 0 + 0 + 0 = 1

(ab1, bc1) = |ab1|*|bc1|*cos(P)

1 = sqrt(2)(sqrt(2)* cos(P)

cos(P) = 1/2

P = 30 гр – искомый угол.

Второй угол совершенно аналогично.

Для решения этой задачи, нам понадобится знание геометрии и некоторых свойств параллельных прямых. Давайте рассмотрим каждый вопрос по отдельности.

1) Чтобы найти угол между прямыми AC и B1D1, нам нужно найти значения их направляющих векторов и воспользоваться формулой для нахождения угла между векторами.

Для прямой AC, направляющие векторы можно найти из координат точек A и C. В данном случае, координаты точки A: A(0, 0, 0), а координаты точки C: C(1, 0, 0). Тогда направляющий вектор прямой AC будет равен AC = C - A = (1, 0, 0) - (0, 0, 0) = (1, 0, 0).

Аналогично, для прямой B1D1, координаты точки B1: B1(1, 1, 1), а координаты точки D1: D1(0, 1, 1). Тогда направляющий вектор прямой B1D1 будет равен B1D1 = D1 - B1 = (0, 1, 1) - (1, 1, 1) = (-1, 0, 0).

Теперь мы можем воспользоваться формулой для нахождения угла между векторами:

cos(угол) = (AC * B1D1) / (|AC| * |B1D1|),

где AC * B1D1 - скалярное произведение векторов AC и B1D1,
|AC| и |B1D1| - длины векторов AC и B1D1 соответственно.

Для нашей задачи:
AC * B1D1 = (1, 0, 0) * (-1, 0, 0) = -1,
|AC| = sqrt(1^2 + 0^2 + 0^2) = 1,
|B1D1| = sqrt((-1)^2 + 0^2 + 0^2) = 1.

Подставим эти значения в формулу:

cos(угол) = (-1) / (1 * 1) = -1.

Значение cos(угла) равно -1. Чтобы найти сам угол, нужно найти арккосинус от -1. Арккосинус(-1) равен pi (или 180 градусов), так как это значение соответствует углу 180 градусов между прямыми AC и B1D1.

Таким образом, угол между прямыми AC и B1D1 равен 180 градусов.

2) Чтобы найти угол между прямыми AD1 и A1B, мы можем воспользоваться тем же методом, что и в предыдущем вопросе.

Направляющие векторы прямой AD1 можно найти из координат точек A и D1. В данном случае, координаты точки A: A(0, 0, 0), а координаты точки D1: D1(0, 1, 1). Тогда направляющий вектор прямой AD1 будет равен AD1 = D1 - A = (0, 1, 1) - (0, 0, 0) = (0, 1, 1).

Аналогично, для прямой A1B, координаты точки A1: A1(1, 0, 0), а координаты точки B: B(1, 1, 0). Тогда направляющий вектор прямой A1B будет равен A1B = B - A1 = (1, 1, 0) - (1, 0, 0) = (0, 1, 0).

Теперь мы можем воспользоваться формулой для нахождения угла между векторами:

cos(угол) = (AD1 * A1B) / (|AD1| * |A1B|),

где AD1 * A1B - скалярное произведение векторов AD1 и A1B,
|AD1| и |A1B| - длины векторов AD1 и A1B соответственно.

Для нашей задачи:
AD1 * A1B = (0, 1, 1) * (0, 1, 0) = 0,
|AD1| = sqrt(0^2 + 1^2 + 1^2) = sqrt(2),
|A1B| = sqrt(0^2 + 1^2 + 0^2) = 1.

Подставим эти значения в формулу:

cos(угол) = 0 / (sqrt(2) * 1) = 0.

Значение cos(угла) равно 0. Чтобы найти сам угол, нужно найти арккосинус от 0. Арккосинус(0) равен pi/2 (или 90 градусов), так как это значение соответствует прямому углу (90 градусов) между прямыми AD1 и A1B.

Таким образом, угол между прямыми AD1 и A1B равен 90 градусов.

3) Для нахождения угла между A1C и AD, мы также можем использовать направляющие векторы соответствующих прямых.

Направляющий вектор прямой A1C можно найти из координат точек A1 и C. В данном случае, координаты точки A1: A1(1, 0, 0), а координаты точки C: C(1, 0, 0). Тогда направляющий вектор прямой A1C будет равен A1C = C - A1 = (1, 0, 0) - (1, 0, 0) = (0, 0, 0), что означает нулевой вектор.

Направляющий вектор прямой AD мы уже вычислили ранее в первом вопросе, он равен AD1 = (0, 1, 1).

Теперь мы можем воспользоваться формулой для нахождения угла между векторами:

cos(угол) = (A1C * AD1) / (|A1C| * |AD1|),

где A1C * AD1 - скалярное произведение векторов A1C и AD1,
|A1C| и |AD1| - длины векторов A1C и AD1 соответственно.

Для нашей задачи:
A1C * AD1 = (0, 0, 0) * (0, 1, 1) = 0,
|A1C| = sqrt(0^2 + 0^2 + 0^2) = 0,
|AD1| = sqrt(0^2 + 1^2 + 1^2) = sqrt(2).

Подставим эти значения в формулу:

cos(угол) = 0 / (0 * sqrt(2)) = 0 / 0.

Значение cos(угла) равно 0 / 0, что является неопределенностью. Это означает, что угол между прямыми A1C и AD1 не может быть вычислен только на основе предоставленной информации.

Таким образом, угол между прямыми A1C и AD1 не может быть определен.