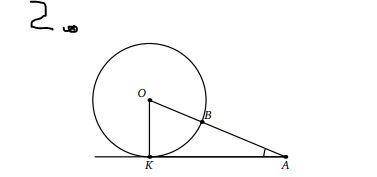
1. Угол при вершине равнобедренного треугольника равен 24. Найдите угол между биссектрисой и высотой этого треугольника, проведёнными к одной и той же боковой стороне. ответ дайте в градусах. (ответ должен быть 27.) 2. Из точки A проведена касательная AK (K — точка касания) к окружности с центром O. Окружность пересекает отрезок AO в точке B. Известно, что tg∠OAK=5/12. Найдите OB/BA. (Рисунок есть, ответ должен быть 0,625.)
Ответы
1. Для решения данной задачи, нам необходимо использовать свойства равнобедренных треугольников.
Обозначим углы равнобедренного треугольника как A, B и C. Поскольку треугольник равнобедренный, то углы A и B смежные и равны между собой.
Угол при вершине C равен 24°, и поскольку два угла равны, каждый из них будет равен половине угла при вершине. То есть, угол A и угол B будут равны 12° каждый.
Теперь, чтобы найти угол между биссектрисой и высотой, проведенными к одной и той же боковой стороне, мы можем использовать следующий факт:
Угол между биссектрисой и высотой, проведенными к одной и той же боковой стороне равнобедренного треугольника, будет равен половине угла при вершине, так же как углы A и B.
Таким образом, угол между биссектрисой и высотой равнобедренного треугольника будет равен 12°.
2. Для решения данной задачи, нам необходимо использовать свойства теоремы о касательной и секущей.
Известно, что tg∠OAK=5/12. Мы знаем, что tg угла равен отношению противолежащего катета к прилежащему катету.
Теперь, чтобы найти OB/BA, мы можем использовать свойства теоремы о касательной и секущей, которая гласит, что касательная и секущая, проведенные из одной точки, образуют квадратичную зависимость.
Известно, что ОА является секущей линией окружности, а ОК является касательной к окружности в точке К. Тогда мы можем записать следующее соотношение:
(OB)^2 = OA * OK
Нам дано, что tg∠OAK=5/12. Используем это соотношение и получим:
tg∠OAK = ОК/ОА = 5/12.
ОК/ОА = 5/12
ОК = (5/12) * ОА
(ОА+АB)^2 = ОА * (5/12) * ОА
(ОА+АB)^2 = (5/12) * (ОА)^2
ОА^2 + 2 * ОА * АB + (АB)^2 = (5/12) * (ОА)^2
ОА^2 + 2 * ОА * АB + (АB)^2 = (5/12) * (ОА)^2
(АB)^2 + 2 * ОА * АB = (5/12) * (ОА)^2
(АB)^2 = (5/12) * (ОА)^2 - 2 * ОА * АB
(АB)^2 = (5/12) * (ОА)^2 - (24/12) * ОА * АB
(АB)^2 = (5/12) * (ОА)^2 - (2/12) * ОА * АB
(АB)^2 = (1/12) * (ОА)^2 - (2/12) * ОА * АB
12 * (АB)^2 = (ОА)^2 - 2 * ОА * АB
12 * (АB)^2 - (ОА)^2 + 2 * ОА * АB = 0
(4 * АB - ОА)^2 = 0
4 * АB - ОА = 0
4 * АB = ОА
АB/ОА = 1/4
Таким образом, OB/BA = AB/OA = 1/4 = 0,25.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Оитию Руси в начале XIV в.? 3. Каким образом московские князья рас-ширяли...
1 - Задание: подчеркните грамматическую основу предложений, укажите вид...
3 - Назвіть етнічні спільноти ,які були у складі Югославії...
3 - Годы правления императора Муцухито.Варианты А)1850-1860 Б)1867-1912...
1 - Чим відрізняється між собою цикл з лічильником і цикл з передумовою...
1 - Рівняння 3 1/8х- (3,5-2х)=3(2.5/6+1 1/3х)...
1 - Чому доктор Брякус запропонував Іванові зайнятися спортом і забороняв...
1 - Решите неравенство, где N – 12а) 3(N+2x)≥N+4+2(x+N);б) (2x+N)-4(x+N)+1...
3 - ответте на во да или нет 1. Автомобили, работающие на газообразном...
3 - Анализ песни Священная война Лебедева-Кумача/Александрова. Какая...
1