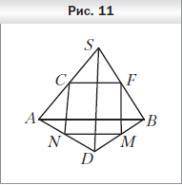
1.Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр. 2. Плоскость β пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN: CB = 3: 4. Найдите сторону AC треугольника

Добрый день! Давайте разберем по очереди заданные вопросы.

1. Чтобы определить вид четырехугольника FMNC, нам необходимо проанализировать его стороны и углы.

- Поскольку F, M, N и C - середины отрезков BS, DB, AD и AS соответственно, мы можем использовать свойство серединных перпендикуляров, которое гласит, что любой отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и составляет с ней половину ее длины.

Из этого свойства следует, что MC || AB, FN || AD, а также FM || BS.

- Также из условия известно, что SD = 30 см и AB = 36 см.

Исходя из всего вышеизложенного, можно заключить:

- Стороны четырехугольника перпендикулярны друг другу:
FM ⊥ MC, MC ⊥ CN, CN ⊥ FN, FN ⊥ FM.

- Стороны FM и FN перпендикулярны стороне AB.

- Стороны MC и CN перпендикулярны стороне AD.

- Стороны FM и MC параллельны стороне BS.

Таким образом, четырехугольник FMNC является прямоугольником.

Чтобы вычислить периметр четырехугольника FMNC, нам необходимо знать длины его сторон. Мы знаем, что AD = AB - 2 * DN и SD = 30 см.

Вычислим стороны четырехугольника:

AB = 36 см (дано в условии)

DN = (3/7) * CB (по условию DN: CB = 3:4)

AD = AB - 2 * DN

= 36 - 2 * ((3/7) * CB)

= 36 - (6/7) * CB

SD = 30 см (дано в условии)

Теперь, чтобы найти периметр, нужно сложить все стороны четырехугольника:

Периметр FMNC = FM + MC + CN + FN

= (FM + FN) + (MC + CN)

= AB + AD + DN + SD

= 36 + (36 - (6/7) * CB) + (3/7) * CB + 30

= 102 + (3/7) * CB - (6/7) * CB

= 102 - (3/7) * CB

Таким образом, периметр четырехугольника FMNC равен 102 - (3/7) * CB.

2. Чтобы найти сторону AC треугольника ABC, нам нужно использовать свойство подобных треугольников и пропорции.

Дано:

AD = 6 см (дано в условии)

DN : CB = 3 : 4 (дано в условии)

Треугольник ABC и треугольник ABD подобны, так как они имеют параллельные стороны: BC || AD.

Значит, соответствующие стороны треугольников подобны в отношении их длин.

Пропорция между сторонами треугольников ABC и ABD:

AC : AD = BC : BD

Подставим известные значения в пропорцию и решим ее относительно AC:

AC : 6 = BC : (BC - DN)

AC = (BC * 6) / (BC - DN)

= (BC * 6) / (BC - (3/7) * CB)

Таким образом, сторона AC треугольника ABC равна (BC * 6) / (BC - (3/7) * CB).

Мне надеюсь, что мой ответ был подробным и полезным для вас. Если у вас возникнут еще вопросы, я с радостью помогу вам!