1) RH-высота треугольника CRЅ. 2)ТМ-биссектриса треугольника NET,
3)AD-биссектриса треугольника AFN
4)TM-медиана треугольника NET.
5) RH-медиана треугольника CRS
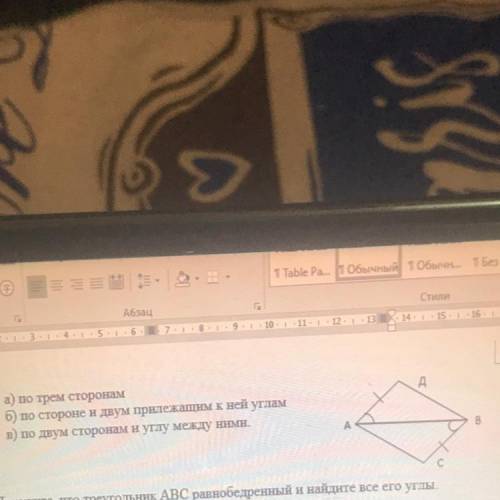
2. Используя рисунок, выясните, по каким элементам треугольник АДВ равен
Треугольнику ACB
а) по трём сторонам
Б) по стороне и двум прилежащим к ней угла
В) по двум сторонам и углу между ними
Другие вопросы по теме Геометрия
Популярные вопросы
- Государство Африки, крупнейший производитель золота...
2 - Государство Африки с наибольшей численностью населения...
3 - Государство - экспортер кукурузы, пшеницы и мяса в Латинской Америке...
1 - Государство - лидер по производству товаров народного потребления и сбору риса...
3 - Государственный язык австралийцев...
2 - Государственный язык Австралийского Союза...
1 - Государства, являющиеся островными...
1 - Государства, не имеющие прямого выхода к морю...
1 - Господство тёмно-зелёных мхов, лишайников, болот характерно для...
2 - Горячий источник, периодически действующий в виде фонтана...
2
1) RH-высота треугольника CRS:
Высота треугольника - это отрезок, проведенный из вершины треугольника к основанию перпендикулярно этой основе. В данном случае, RH является высотой треугольника CRS.
2) TM-биссектриса треугольника NET:
Биссектриса треугольника - это отрезок, который делит угол треугольника на две равные части. В данном случае, TM является биссектрисой треугольника NET.
3) AD-биссектриса треугольника AFN:
Аналогично предыдущему пункту, AD является биссектрисой треугольника AFN.
4) TM-медиана треугольника NET:
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае, TM является медианой треугольника NET.
5) RH-медиана треугольника CRS:
Аналогично предыдущему пункту, RH является медианой треугольника CRS.
Теперь перейдем к решению задачи.
Исходя из предоставленного рисунка, нам нужно выяснить, по каким элементам треугольник АДВ равен треугольнику ACB.
а) По трём сторонам:
Для того чтобы сказать, что треугольники равны по трём сторонам, нужно убедиться в равенстве всех трех сторон двух треугольников. При нашей предоставленной информации это сделать невозможно, так как у нас нет информации о длинах сторон треугольников.
б) По стороне и двум прилежащим к ней угла:
В данном случае, треугольники будут равны, если у них будет равна одна сторона и два прилежащих к ней угла. Как видно на рисунке, сторона AD равна стороне AC, а также угол ADF равен углу ACE и угол DAF равен углу EAC. Поэтому, треугольники АДВ и АСВ равны по стороне AD и двум прилежащим к ней углам.
в) По двум сторонам и углу между ними:
Для того чтобы треугольники были равны по двум сторонам и углу между ними, длины этих сторон и величина угла между ними должны быть равными. На рисунке видно, что стороны AD и AC равны, а угол DAF равен углу EAC. Поэтому, треугольники АДВ и АСВ равны по двум сторонам AD и AC и углу между ними.
Таким образом, треугольники АДВ и АСВ равны по стороне и двум прилежащим к ней углам, а также по двум сторонам и углу между ними.