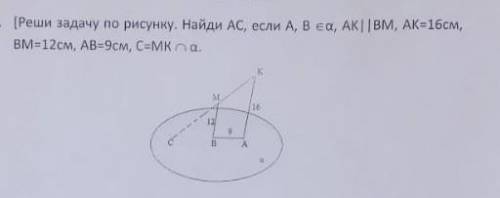
1. [Реши задачу по рисунку. Найди AC, если A, B пренадлежит a, AK | | ВМ, АК=16см, BM=12 , AB=9cm, C=MK a

Для решения задачи, нам необходимо использовать параллельные прямые и пропорциональные отрезки.

1. Нам дано, что отрезок AK параллелен отрезку BM, поэтому углы AMK и ABM являются соответственными углами и равны.

2. Мы также знаем, что AB и BM имеют заданные значения: AB = 9 см, BM = 12 см.

3. Используя формулу соответственных сторон прямоугольного треугольника, мы можем найти часть отрезка AK, соответствующую отрезку AB.

AB/AM = BM/AK

9/AM = 12/16
16 * 9 = 12 * AM
AM = (16 * 9) / 12
AM = 12

Таким образом, AM = 12 см.

4. Теперь мы можем использовать найденное значение AM и отрезок AB, чтобы найти отрезок AC.

Известно, что отрезок AC = AM + MC.

Мы знаем, что AM = 12 см, и нам нужно найти MC.

Используя пропорциональность отрезков, мы можем установить следующее: AB/MC = AM/BM. Подставим известные значения: 9/MC = 12/12. Заметим, что BM и MC равны.

MC * 9 = 12 * 12
MC = (12 * 12) / 9
MC = 16

Таким образом, MC = 16 см.

5. Теперь мы можем найти отрезок AC, сложив AM и MC.

AC = AM + MC
AC = 12 + 16
AC = 28

Ответ: AC = 28 см.