1. Отрезки делятся пополам, значит, KP = ,
= LP,
∡
= ∡ MPL, так как прямые перпендикулярны и каждый из этих углов равен
°.
По первому признаку равенства треугольник KPN равен треугольнику MPL.
2. В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие ∡
и ∡ M, ∡
и∡ L.
∡ K =
°;
∡ N =
°.
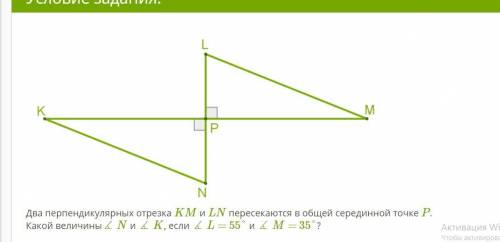
Другие вопросы по теме Геометрия
Популярные вопросы
- Какую окраску имеют в растворе соляной кислоты индикаторы: а) лакмус, б) метилоранж,...
1 - Случайная величина x принимает два значения x1=2 и x2=3, имеет математическое...
2 - В 1000 г воды растворили 224 л (н.у.) хлороводорода. Определите массовую долю...
1 - Расскажите о правилах работы с концентрированной серной кислотой. Почему при...
1 - Определите объем (н.у.) углекислого газа СO2, который образуется при действии...
1 - Напишите электронную формулу атома кислорода. Сколько неспаренных электронов...
3 - Функция спроса задана уравнением: Q(d)=3000-6P 1) выведите формулу эластичности...
3 - В ходе реакции 11,7 г хлорида натрия и избытка концентрированной серной кислоты...
2 - Как меняются в группе сверху вниз радиус атомов, их электроотрицательность,...
1 - Напишите уравнения возможных реакций соляной кислоты со следующими веществами:...
3
1. Первый шаг: Отрезки KP и LP делятся пополам, поэтому мы можем сказать, что KP равно LP. Это верно, потому что когда отрезки делятся пополам, они становятся равными частями одного целого.
2. Второй шаг: Мы знаем, что угол M равен углу P, а угол L равен углу N. Это верно, потому что прямые, на которых лежат эти углы, являются перпендикулярными, и когда две прямые пересекаются, образуется система вертикальных углов, которые равны.
3. Третий шаг: По первому признаку равенства треугольник KPN равен треугольнику MPL. Доказательство этого факта заключается в следующем: у нас есть две стороны KP и LP, которые равны, и у нас есть углы K и P, которые также равны. Следовательно, мы можем применить первый признак равенства треугольников SSA (сторона-сторона-угол) и сказать, что треугольник KPN равен треугольнику MPL.
4. Четвертый шаг: Мы знаем, что ∡ K равен ∡ P и ∡ N равен ∡ L. Так как треугольник KPN равен треугольнику MPL, то соответствующие углы также равны. Это значит, что ∡ K равно ∡ M и ∡ N равно ∡ L. В данном случае, ∡ K равно 60 градусам и ∡ N равно 45 градусам, поэтому можно сказать, что ∡ M равно 60 градусам и ∡ L равно 45 градусов.
В итоге, мы доказали, что отрезки KP и LP делятся пополам, углы K и P равны, а углы N и L равны. Таким образом, можно сделать вывод, что треугольник KPN равен треугольнику MPL.