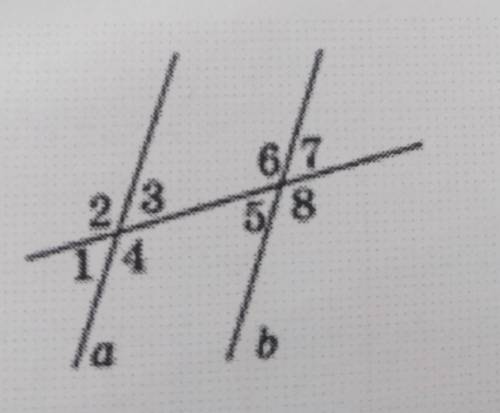
1. Объясните, почему
прямые а и b параллельны
(см. рисунок),​

Чтобы объяснить, почему прямые а и b параллельны, нужно рассмотреть их угловую величину и свойства параллельных прямых.

Прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются. На рисунке видно, что прямые а и b не пересекаются и идут в одном направлении. Это одно из свойств параллельных прямых - они имеют одинаковое направление.

Для доказательства, что а и b являются параллельными, можно воспользоваться двумя точками: точкой A на прямой а и точкой C на прямой b.

Затем с помощью линейки можно провести линию от точки A до точки C, чтобы получить третью прямую, обозначим ее как с.

Однако, так как а и b - параллельные прямые, то прямая с будет параллельна каждой из них.

Теперь рассмотрим углы между прямыми. Угол BAC и угол BСА считаются соответственно вертикальными, так как они лежат на пересекающихся прямых. Также, угол ABC и угол ВСD считаются соответственно вертикальными, так как они лежат на пересекающихся прямых.

Однако, так как прямые а и b - параллельные, углы между ними будут соответственными, то есть они будут равны. В данном случае углы BAC и ВСD будут равны.

Таким образом, мы доказали, что углы между прямыми а и b равны и параллельные прямые имеют одинаковое направление. Исходя из этих свойств, мы можем сделать вывод, что прямые а и b являются параллельными.