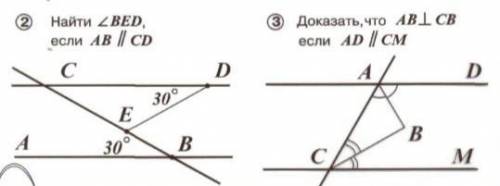
1.найти угол BED,если AB || CD
2.доказать,что AB перпендикулярно CB если AD||CM​

1. Для нахождения угла BED в данной задаче, мы можем использовать свойство параллельных прямых и треугольников, образованных этими прямыми.

Обратим внимание, что у нас есть две параллельные прямые: AB и CD. По свойству параллельных прямых, соответственные углы при пересечении этих прямых равны.

Таким образом, угол DAB равен углу ECD.

Теперь рассмотрим треугольник ABE. В этом треугольнике есть два известных угла: угол BED и угол DAB (который равен углу ECD). Зная эти два угла, мы можем найти третий угол суммой углов треугольника.

Сумма углов треугольника равна 180 градусам. Известно, что угол DAB равен 71 градусу, так как он равен углу ECD. Зная это, мы можем использовать формулу для нахождения угла BED:

Угол BED = 180 - угол DAB - угол EBD
Угол BED = 180 - 71 - 35
Угол BED = 74 градуса

Таким образом, угол BED равен 74 градусам.

2. Для доказательства того, что AB перпендикулярно CB, если AD || CM, мы можем использовать свойство параллельных прямых и перпендикуляра.

В данной задаче у нас две параллельные прямые: AD и CM.

Теперь посмотрим на треугольник ABC. Поскольку AD || CM, углы CDA и MCB являются соответственными углами. Из свойства параллельных прямых следует, что эти углы равны.

Далее рассмотрим треугольник ABC. У нас есть угол CDA, который равен углу MCB (из предыдущего рассуждения). Также у нас есть угол BAC (или угол A) и угол ACB (или угол C), образованные прямолинейными углами.

Если AB перпендикулярно CB, то угол BAC должен быть равен 90 градусам. Для доказательства этого, рассмотрим сумму углов треугольника ABC:

Сумма углов треугольника равна 180 градусам. У нас уже известны углы CDA и MCB, которые равны друг другу. Пусть это значение равно Х.

Теперь применим операцию вычитания: 180 - Х - Y = 0, где Х и Y - значения углов.

Заметим, что Y это угол BAC, который мы хотим доказать, что равен 90 градусам. Подставим это значение в наше уравнение:

180 - Х - 90 = 0

Упростим это уравнение:

90 - Х = 0

Х = 90

Таким образом, угол BAC равен 90 градусам.

Это доказывает, что AB перпендикулярно CB, если AD || CM.