1) Найти соs71 градуса. 2) Найти cos18 гр 25минут. 3)В треугольнике АВС с=14 см, угол А равен 60 гр. Найти радиус описанной окружности.

1) cos 71° = 0,3256.

2) cos 18° 25' = 0,9488.

3) Радиус описанной окружности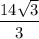 см.

Объяснение:

1) Найти cos 71°.

Воспользуемся таблицами Брадиса В.М. для синусов и косинусов углов.

Для нахождения косинусов углов таблицу используем снизу вверх, значения углов берем из правой колонки, значения минут из нижней строки.

Находим значение cos 71° 0' (см. приложение 1).

cos 71° = 0,3256.

2) Найти cos 18° 25'.

Находим по таблице косинусов в правой колонке угол 18°.

В нижней строке нет значения 25', поэтому берем ближайшее значение минут: 24', и сделаем поправку на 1 минуту. Поправка равна 1 (см. приложение 2).

cos 18° 24' = 0,9489.

Так как с увеличением острого угла значение косинуса уменьшается, то поправку нужно отнять.

9489 - 1 = 9488.

Тогда cos 18° 25' = 0,9488.

3) Найти радиус описанной около треугольника окружности, если известен угол треугольника ∠A = 60° и длина противолежащей стороны BC = 14 см.
Рисунок прилагается (приложение 3).

Радиус описанной окружности найдем по формуле:

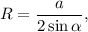
где R - радиус описанной окружности, a - сторона треугольника, α - противолежащий этой стороне угол.

По таблице:

Подставим данные задачи:

(см).

Радиус описанной окружности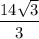 см.