1) найдите площадь квадрата, если радиус описанной около него окружности равен 2 дм. 2) найдите сторону квадрата, если расстояние от его центра до вершины равно 2 дм. 3) найдите радиус окружности, вписанной в квадрат, если радиус
описанной около него окружности равен 2 дм. ! хотя бы одну ((

Ответы

valeriaovsiann 24.05.2020 00:33

№1.

$S=a^2=(R\sqrt2)^2=2R^2=2\cdot2^2=8$ (кв.дм)

ответ: площадь квадрата 8 квадратных дециметров.

№2.

Расстояние от центра до вершина составляет половину диагонали квадрата, длина диагонали равна d=2*2=4 (дм)

По теоереме Пифагора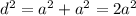 d^2=a^2+a^2=2a^2

$a=\sqrt{\frac{d^2}{2}}=\sqrt{\frac{4^2}{2}}=\sqrt8=2\sqrt2$ (дм)

ответ: сторона квадрата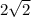 $2\sqrt2$ дециметра.

№3.

R - радиус описанной окружности, r - радиус вписанной окружности

$a=R\sqrt2$

$r=\frac{a}{2}=\frac{R\sqrt2}{2}=\frac{2\sqrt2}{2}=\sqrt2$ (дм)

ответ: радиус окружности, вписанной в квадрат,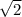 $\sqrt2$ дециметра.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

DISTANOV 07.09.2019 17:50

mama1488 07.09.2019 17:50

Metyakarimi 07.09.2019 17:50

cimuzoro 07.09.2019 17:50

ашпшплщ 07.09.2019 17:50

Маркіза1 05.07.2019 17:30

refdiamond 05.07.2019 17:30

aizhanashoznweb 05.07.2019 17:30

vazirasharipovа 03.06.2021 08:44

FJFJKD99 03.06.2021 08:56