1. Найдите координаты точек, симметричных точке B (2; 4; -5). a) плоскости XY, б) оси Х, в) начала координат.
2. Дан треугольник ABC с вершинами (11; -2; -9), В(2; 6; -4), С(14; 2; -10).
а) найдите координаты середины отрезка ВС,
б) найдите координаты и модуль вектора ВС,
с) найдите вектор АВ + ВС, докажите перпендикулярность вектора АВ и АС.
3. Дан вектор а (2; 1; -2)
а) известно, что a = EF,
Найдите координаты точки F, если Е (2; 0; 3),
б) Найдите значения m и n, при которых векторы а и b коллинеарны, если b (m; n; -4),
в) Найдите координаты и модуль вектора с, если с = -3а.
4. Даны векторы а(-2; -2; 1), b(0; -4; 3)
а) Найдите вектор
б) Найдите (a + b) (a - b),
в) Найдите косинус угла между векторами а и b.
5. Докажите что четырёхугольник параллелограмм, и найдите его центр симметрии, если A(-1;4;3), B(-3;6;-5), C(3;0;-5), P(5; -2;3).
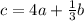
Другие вопросы по теме Геометрия
Популярные вопросы
- написать сочинение по плану и по картинке. 3-4 столбца. Благодарю за...
3 - Дельфин поднялся над водой на высоту h=1,5м имея при скорость 2,0 с...
1 - Отже, що насправді змушує людей жити довше?...
3 - людина піднімає за 16 с із колодязя завглибшки 8м відро масою 10кг....
3 - Всесвітня історія: Назвіть основні технічні винаходи та наукові відкриття...
2 - Знайдіть периметер палелограми а) 1,3м б) 0,65м в) 2,6м г) 0,4²...
1 - ДО ІТЬ БУДЬ-ЛАСКАУСТАНОВІТЬ ВІДПОВІДНІСТЬМІЖ ВІДОКРЕМЛЕНИМ ЧЛЕНОМ РЕЧЕННЯТА...
3 - Упражнения 5 Фототю прикрепил Допишите её закончив предложение. Поставьте...
1 - Футбольний м’яч після удару набув кінетичної енергії 60 Дж. У верхній...
3 - візок масою 20кг рухається по горизонтальній поверхні прямолінійно...
3
a) Для нахождения координат точки, симметричной точке B (2; 4; -5) относительно плоскости XY, нужно сохранить первые две координаты (X и Y) неизменными, а изменить знак третьей координаты (Z). Таким образом, точка B' будет иметь координаты (2; 4; 5).
b) Для нахождения координат точки, симметричной точке B (2; 4; -5) относительно оси X, нужно сохранить первую координату (X) неизменной, а изменить знак второй и третьей координаты (Y и Z). Таким образом, точка B' будет иметь координаты (2; -4; 5).
c) Для нахождения координат точки, симметричной точке B (2; 4; -5) относительно начала координат, нужно изменить знак всех трех координат. Таким образом, точка B' будет иметь координаты (-2; -4; 5).
2.
a) Чтобы найти координаты середины отрезка ВС, нужно просуммировать соответствующие координаты точек В и С и разделить полученные суммы на 2.
x-координата середины отрезка ВС: (2+14)/2 = 8
y-координата середины отрезка ВС: (6+2)/2 = 4
z-координата середины отрезка ВС: (-4-10)/2 = -7
Таким образом, координаты середины отрезка ВС равны (8; 4; -7).
б) Чтобы найти вектор ВС, нужно вычесть соответствующие координаты точек С и В.
Вектор ВС = (14-2; 2-6; -10-(-4)) = (12; -4; -6)
Модуль вектора ВС можно найти по формуле модуля вектора: ||ВС|| = √(12^2 + (-4)^2 + (-6)^2) = √(144 + 16 + 36) = √196 = 14
с) Чтобы найти вектор АВ + ВС, нужно сложить соответствующие координаты векторов АВ и ВС.
Вектор АВ = (2-11; 6-(-2); -4-(-9)) = (-9; 8; 5)
Вектор ВС = (12; -4; -6)
Вектор АВ + ВС = (-9+12; 8-4; 5-6) = (3; 4; -1)
Для доказательства перпендикулярности векторов АВ и АС используем свойство скалярного произведения векторов: если для двух векторов их скалярное произведение равно нулю, то они перпендикулярны.
Вектор АВ * Вектор АС = (-9; 8; 5) * (11-2; -2-6; -9-(-4)) = (-9; 8; 5) * (9; -8; -5) = (-9*9 + 8*(-8) + 5*(-5)) = (-81 + (-64) + (-25)) = (-170)
Так как скалярное произведение векторов АВ и АС равно -170, а не равно нулю, значит, векторы АВ и АС не являются перпендикулярными.
3.
a) Для нахождения координат точки F, если известно, что a = EF, нужно от точки E отнять вектор а.
E (2; 0; 3)
а (2; 1; -2)
Координаты точки F равны (2-2; 0-1; 3-(-2)) = (0; -1; 5).
б) Чтобы векторы а и b были коллинеарными, должно выполняться условие, что они имеют одинаковое отношение своих координат.
Запишем соответствующие координаты векторов а и b:
a (2; 1; -2)
b (m; n; -4)
Произведем пропорцию координат:
2/m = 1/n = -2/(-4)
Из первого равенства получаем m = 2n, а из второго равенства получаем -4 = 2n, что дает n = -2.
Таким образом, при значениях m = 4 и n = -2 векторы а и b будут коллинеарными.
в) Чтобы найти координаты и модуль вектора с, если с = -3а, нужно умножить каждую координату вектора а на -3.
а (2; 1; -2)
с (-6; -3; 6)
Модуль вектора с можно найти по формуле модуля вектора: ||с|| = √((-6)^2 + (-3)^2 + 6^2) = √(36 + 9 + 36) = √81 = 9.
4.
a) Чтобы найти вектор c = 4a + (1/3)b, нужно умножить каждую координату вектора а на 4, каждую координату вектора b на (1/3) и сложить соответствующие координаты.
a (-2; -2; 1)
b (0; -4; 3)
c = 4a + (1/3)b = 4(-2; -2; 1) + (1/3)(0; -4; 3) = (-8; -8; 4) + (0; -4/3; 1) = (-8+0; -8-4/3; 4+1) = (-8; -32/3; 5)
б) Чтобы найти (a + b) (a - b), нужно сначала вычислить сумму и разность векторов а и b, а затем умножить их.
а (-2; -2; 1)
b (0; -4; 3)
(a + b) (a - b) = (-2; -2; 1) + (0; -4; 3) * (-2; -2; 1) - (0; -4; 3) = (-2+0; -2-4; 1+3) * (-2; -2; 1) - (0; -4; 3) = (-2; -6; 4) * (-2; -2; 1) - (0; -4; 3) = (-2*(-2); -6*(-2); 4*1) - (0; -4; 3) = (4; 12; 4) - (0; -4; 3) = (4-0; 12-(-4); 4-3) = (4; 16; 1)
в) Чтобы найти косинус угла между векторами а и b, воспользуемся формулой косинуса угла между векторами:
cosθ = (а * b) / (||а|| * ||b||)
Где а * b - скалярное произведение векторов, ||а|| и ||b|| - модули векторов.
а (-2; -2; 1)
b (0; -4; 3)
а * b = (-2*0 + -2*(-4) + 1*3) = (0 + 8 + 3) = 11
||а|| = √((-2)^2 + (-2)^2 + 1^2) = √(4 + 4 + 1) = √9 = 3
||b|| = √(0^2 + (-4)^2 + 3^2) = √(0 + 16 + 9) = √25 = 5
cosθ = (11) / (3*5) = 11/15
Таким образом, косинус угла между векторами а и b равен 11/15.
5.
Чтобы доказать, что четырехугольник ABCP - параллелограмм, нужно проверить, что противоположные стороны попарно равны.
Вектор AB = (11-(-1); -2-4; -9-3) = (12; -6; -12)
Вектор BC = (14-11; 2-(-2); -10-(-9)) = (3; 4; -1)
Вектор CP = (5-14; -2-2; 3-(-10)) = (-9; -4; 13)
Вектор PA = (-1-5; 4-(-2); 3-3) = (-6; 6; 0)
Проверяем равенство:
AB = CP: (12; -6; -12) = (-9; -4; 13) - DA
BC = PA: (3; 4; -1) = (-6; 6; 0) + DA
Так как оба условия выполняются, можно сделать вывод, что четырехугольник ABCP - параллелограмм.
Для нахождения центра симметрии четырехугольника, нужно найти среднюю точку между диагоналями.
Диагональ AC = (14-(-1); 2-4; -10-3) = (15; -2; -13)
Диагональ BP = (5-(-3); -2-6; 3-(-5)) = (8; -8; 8)
Суммируем диагонали и делим их на 2:
(15+8)/2 = 23/2
(-2-8)/2 = -10/2 = -5
(-13+8)/2 = -5/2
Таким образом, координаты центра симметрии четырехугольника ABCP равны (23/2; -5; -5/2).