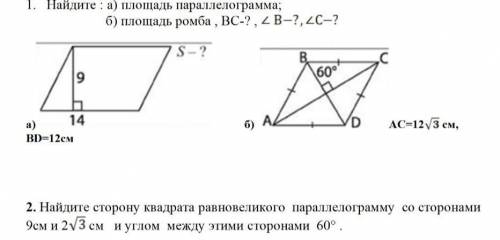
1. Найдите : а) площадь параллелограмма; б) площадь ромба , ВС-? , B-?, C-? а)BD=12см б)AC=12√3 2. Найдите сторону квадрата равновеликого параллелограмму со сторонами 9см и 2√3см и углом между этими сторонами 60° .

Добрый день! Давайте решим эту задачу по порядку.

1. а) Для нахождения площади параллелограмма необходимо знать длину одной из его сторон и высоту, проведенную к этой стороне. В данном случае, если известна длина стороны BD (12 см), то для нахождения площади нужно найти длину высоты проведенной к стороне BD.

Поскольку параллелограммы имеют противоположные стороны, равные и параллельные друг другу, высота, проведенная к стороне BD, равна высоте, проведенной к стороне AC. Следовательно, если длина стороны AC известна (12√3), мы можем использовать ее для нахождения высоты параллелограмма.

Так как дано, что угол между сторонами AC и BD равен 90°, высоту параллелограмма можно найти по формуле h = AC * sin(угол между сторонами). Подставим известные данные:

h = (12√3) * sin(90°)
h = 12√3 * 1
h = 12√3

Теперь, когда мы знаем высоту параллелограмма (12√3) и длину стороны BD (12 см), мы можем найти площадь:

S = BD * h
S = 12 * 12√3
S = 144√3 см^2

Ответ: площадь параллелограмма равна 144√3 см^2.

1. б) Теперь найдем площадь ромба, зная его сторону ВС (будем обозначать БС). Для этого нужно знать длину одной из диагоналей ромба и угол между диагоналями.

В данной задаче нам дана длина стороны AC (12√3) и нам нужно найти длину диагонали ВС (будем обозначать СВ), а также длины отрезков ВB, BC и CA.

Поскольку угол между сторонами АС и BD равен 90°, и также угол между диагоналями ВС и BD равен 90°, то треугольник АВD - прямоугольный треугольник. Также треугольник DСA - прямоугольный треугольник, так как противоположные стороны в ромбе равны.

По теореме Пифагора, в прямоугольных треугольниках сумма квадратов катетов равна квадрату гипотенузы. Используя это свойство, мы можем найти длину отрезков ВB, BC и CA.

В треугольнике АВD, катеты равны ВB и BD, а гипотенуза равна АD. Используя теорему Пифагора, мы можем записать уравнение:

(ВB)^2 + (BD)^2 = (AD)^2

(ВB)^2 + 12^2 = (9)^2
(ВB)^2 = 81 - 144 = -63

Не забывайте, что отрицательного остатка у квадратного корня быть не может, поэтому у нас нет решения для длины отрезка ВB.

Теперь рассмотрим треугольник DСA. Катет АD равен 9 см, а катет DC равен длине стороны AC, равной 12√3 см. По теореме Пифагора, мы можем записать уравнение:

(12√3)^2 + (DC)^2 = (AC)^2

432 + (DC)^2 = (12√3)^2
432 + (DC)^2 = 432 * 3
(DC)^2 = 432 * 3 - 432 = 864
(DC)^2 = 864

Теперь найдем длину отрезка DC, извлекая квадратный корень:

DC = √864
DC = √(36 * 24)
DC = √36 * √24
DC = 6 * √(4 * 6)
DC = 6 * 2 * √6
DC = 12√6

Теперь у нас есть длина отрезка DC (12√6) и длина отрезка AC (12√3). Используя формулу для нахождения площади ромба: S = (AC * DC)/2, мы можем найти площадь ромба:

S = (12√6 * 12√3)/2
S = (12 * 12 * √6 * √3)/2
S = 144 * √18
S = 144 * 3√2

Ответ: площадь ромба равна 432√2.

2. Найдем сторону квадрата, равновеликого параллелограмму со сторонами 9 см и 2√3 см и углом между этими сторонами 60°.

Если параллелограмм и квадрат равновеликие, то их площади должны быть равны. Поэтому, чтобы найти сторону квадрата, мы будем использовать площади.

Площадь параллелограмма равна 9 см * 2√3 см * sin(60°).
S_параллелограмма = 9 * 2√3 * sin(60°)
S_параллелограмма = 18√3 * (√3/2)
S_параллелограмма = 9√3 * √3
S_параллелограмма = 9 * 3
S_параллелограмма = 27 см^2

Площадь квадрата равна сторона квадрата в квадрате.
S_квадрата = сторона^2

Из условия равновеликости параллелограмма и квадрата, мы должны приравнять их площади:
S_параллелограмма = S_квадрата
27 = сторона^2

Теперь найдем сторону квадрата, извлекая квадратный корень:
сторона = √27
сторона = √(9 * 3)
сторона = 3 * √3

Ответ: сторона квадрата, равновеликого параллелограмму со сторонами 9 см и 2√3 см и углом между этими сторонами 60°, равна 3√3 см.

Надеюсь, мое объяснение было понятным и полезным. Если есть еще вопросы, обращайтесь!