1. Начертите вектор x такой, что |x|=2см. Постройте векторы 3x , -2x , 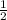x. 2. В параллелограмме ABCD на стороне AB отмечена точка K так, что AK:KB = 2:1, O - точка пересечения диагоналей. Выразите векторы OC и CK через векторы a=AB и b=AD.

1. Начертите вектор x такой, что |x|=2см. Постройте векторы 3x , -2x , 1/2 x.

Для начала построим вектор x длиной 2 см. Для этого нужно нарисовать отрезок такой длины.

Затем, чтобы построить векторы 3x и -2x, нужно умножить вектор x на соответствующие числа.

- Вектор 3x будет иметь длину, равную длине вектора x, умноженной на число 3. То есть, 3x будет иметь длину 6 см. Нарисуем вектор, который имеет направление исходного вектора x, но длину в 3 раза больше.

- Вектор -2x будет иметь длину, равную длине вектора x, умноженной на число -2. То есть, -2x будет иметь длину 4 см. Нарисуем вектор, который имеет противоположное направление исходного вектора x, но длину в 2 раза больше.

- Для построения вектора 1/2 x нужно умножить длину вектора x на число 1/2. То есть, 1/2 x будет иметь длину 1 см. Нарисуем вектор, который имеет направление исходного вектора x, но длину в 2 раза меньше.

2. В параллелограмме ABCD на стороне AB отмечена точка K так, что AK:KB = 2:1, O - точка пересечения диагоналей. Выразите векторы OC и CK через векторы a=AB и b=AD.

Для выражения вектора OC через векторы a и b, можно воспользоваться свойствами параллелограмма.

- Вектор OC можно представить как сумму векторов OA и AC. Вектор OA совпадает с вектором OB, так как они являются диагоналями параллелограмма. То есть, OC = OA + AC = OB + AC.

- Вектор AC равен вектору b, так как AC - это одна из сторон параллелограмма, и b является вектором, соответствующим этой стороне.

- Вектор OB равен вектору a, так как OB - это другая сторона параллелограмма, и a является вектором, соответствующим этой стороне.

Таким образом, OC = OA + AC = OB + AC = a + b.

Для выражения вектора CK через векторы a и b, можно воспользоваться тем же свойством параллелограмма.

- Вектор CK можно представить как разность векторов CA и AK. Вектор CA равен вектору -b, так как он обратно направлен к вектору AC.

- Вектор AK равен 2/3 вектора AB, так как AK:KB = 2:1. То есть, вектор AK в 2 раза короче вектора AB. Найдем вектор CK: CK = CA - AK = -b - 2/3 a.

Таким образом, получаем выражения для векторов OC и CK через векторы a и b:
OC = a + b
CK = -b - 2/3 a.