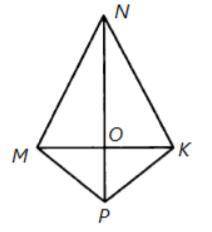
1. На рисунке MP=PK и ∠MPO=∠KPO. Докажите, что ∆ = ∆�

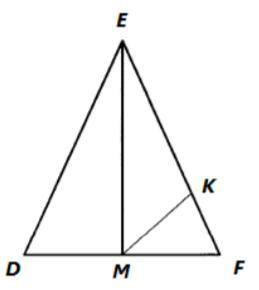
2.На рисунке DE=EF и DM=MF. MK –

биссектриса треугольника MEF. Найдите угол

DMK.

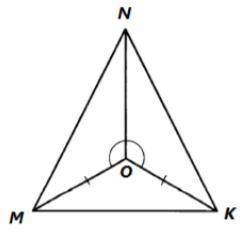
3.На рисунке ∠MON=∠KON, MO=OK.

Докажите, что NO⊥MK

4. В равнобедренном треугольнике DEF с основанием EF=8 см отрезок

DK является биссектрисой. Угол DEK равен 36 градусов. Найдите KF,

угол EDF, угол DKE.

5. На отрезке MN по одну сторону от него построены равнобедренные

треугольники AMN и BMN. Вершины треугольников соединены прямой

AB. Докажите, что AB⊥MN.

1. На рисунке дано, что MP=PK и ∠MPO=∠KPO. Мы должны доказать, что треугольники ΔMPO и ΔKPO равны.

Докажем это пошагово:

Шаг 1: Из условия известно, что MP=PK. Это значит, что отрезки MP и PK имеют одинаковую длину.

Шаг 2: Также из условия известно, что ∠MPO=∠KPO. Это означает, что углы ∠MPO и ∠KPO имеют одинаковую меру.

Шаг 3: Теперь мы знаем, что у нас есть две стороны треугольников, которые равны (MP=PK) и один угол, который имеет одинаковую меру (∠MPO=∠KPO). Согласно свойству треугольников, это достаточно для того, чтобы утверждать, что треугольники ΔMPO и ΔKPO равны.

2. На рисунке DE=EF и DM=MF. MK – биссектриса треугольника MEF. Нам нужно найти угол DMK.

Давайте решим это задание:

Шаг 1: Из условия DE=EF мы знаем, что отрезки DE и EF имеют одинаковую длину.

Шаг 2: Также из условия DM=MF мы знаем, что отрезки DM и MF имеют одинаковую длину.

Шаг 3: Мы знаем, что MK - биссектриса треугольника MEF. Это значит, что угол DMK делит угол EMF пополам.

Шаг 4: Из шага 3 следует, что угол DMK равен половине угла EMF.

3. На рисунке ∠MON=∠KON, MO=OK. Нам нужно доказать, что NO ⊥ MK.

Докажем это пошагово:

Шаг 1: Из условия ∠MON=∠KON мы знаем, что углы ∠MON и ∠KON имеют одинаковую меру.

Шаг 2: Также из условия MO=OK мы знаем, что отрезки MO и OK имеют одинаковую длину.

Шаг 3: Мы знаем, что у нас есть два угла, которые имеют одинаковую меру (∠MON=∠KON) и два отрезка, которые имеют одинаковую длину (MO=OK). Согласно свойству треугольников, это достаточно для того, чтобы утверждать, что треугольники ΔMON и ΔKON равны.

Шаг 4: Если треугольники ΔMON и ΔKON равны, то это означает, что стороны NO и NK имеют одинаковую длину и углы ∠MNO и ∠KNO имеют одинаковую меру.

Шаг 5: У нас есть стороны NO и NK, которые имеют одинаковую длину и углы ∠MNO и ∠KNO, которые имеют одинаковую меру. Это достаточно для того, чтобы утверждать, что сторона NO ⊥ MK.

4. В равнобедренном треугольнике DEF с основанием EF=8 см отрезок DK является биссектрисой. Угол DEK равен 36 градусов. Нам нужно найти KF, угол EDF и угол DKE.

Давайте решим это задание:

Шаг 1: У нас есть равнобедренный треугольник DEF с основанием EF=8 см. Это означает, что отрезки DE и DF имеют одинаковую длину.

Шаг 2: Мы также знаем, что DK является биссектрисой угла DEF. Это значит, что угол DEK делит угол DEF пополам.

Шаг 3: Из шага 2 следует, что угол DEK равен половине угла DEF.

Шаг 4: Мы знаем, что угол DEK равен 36 градусов. Следовательно, угол DEF будет равен 2*36=72 градусов.

Шаг 5: Чтобы найти KF, нам нужно знать отношение длин сторон в равнобедренном треугольнике DEF. Если DE=DF=8 см, то KF будет равно 8/2=4 см.

5. На отрезке MN по одну сторону от него построены равнобедренные треугольники AMN и BMN. Вершины треугольников соединены прямой AB. Нам нужно доказать, что AB ⊥ MN.

Докажем это пошагово:

Шаг 1: У нас есть равнобедренные треугольники AMN и BMN, построенные по одну сторону от отрезка MN. Это означает, что стороны AM и AN равны, а стороны BM и BN также равны.

Шаг 2: Вершины треугольников AMN и BMN соединены прямой AB.

Шаг 3: Чтобы доказать, что AB ⊥ MN, нам нужно показать, что прямая AB перпендикулярна к отрезку MN. Для этого достаточно показать, что угол ABM равен углу AMN или что угол ABN равен углу ANM.

Шаг 4: Из шага 1 следует, что стороны AM и AN равны. Из шага 3 следует, что угол ABM равен углу AMN. Следовательно, угол ABM равен углу AMN.

Шаг 5: Из шага 1 следует, что стороны BM и BN равны. Из шага 3 следует, что угол ABN равен углу ANM. Следовательно, угол ABN равен углу ANM.

Шаг 6: Мы выяснили, что угол ABM равен углу AMN и угол ABN равен углу ANM. Это означает, что прямая AB перпендикулярна к отрезку MN. Следовательно, AB ⊥ MN.