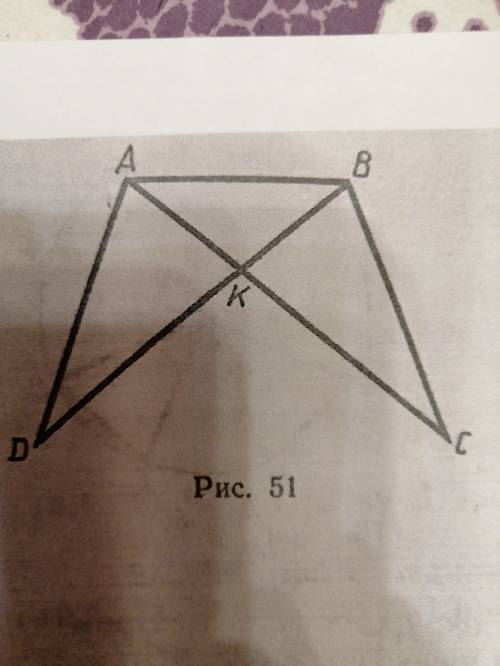
1)На рисунке 51 угол DAB = ABC, AK = KB. Докажите, что угол ADB = BCA.

1)

На рисунке 2.14 угол DAC = DBC, AK = KB. Докажите, что угол DAB = CBA

2)

Точки C и D расположены по разные стороны от прямой AB так,что угол ABC=углу ABD. BD=BC. Докажите что AB- биссектриса угла DAC.

Добрый день! Обратимся к данной задаче.

У нас дано следующее:
1) Угол DAB равен углу ABC.
2) AK равно KB.

Нам нужно доказать, что угол ADB равен углу BCA.

Давайте рассмотрим данное изображение:

B
/ \
/ \
K --------- A
\ /
\ /
\ D /

Для начала, давайте посмотрим на треугольники ADB и BCA.

В треугольнике ADB у нас есть следующие стороны:
1) DA (сторона, общая для обоих треугольников)
2) AK (задано в условии)
3) AD (сторона, общая для обоих треугольников)

В треугольнике BCA у нас есть следующие стороны:
1) BA (сторона, общая для обоих треугольников)
2) BK (задано в условии)
3) BC (сторона, общая для обоих треугольников)

Теперь давайте посмотрим на углы треугольников.

В треугольнике ADB у нас есть следующие углы:
1) угол ADB (задача требует доказать, что он равен углу BCA)
2) угол ABD (образован стороной BA и стороной AD)
3) угол BAD (задано в условии, что угол DAB равен углу ABC)

В треугольнике BCA у нас есть следующие углы:
1) угол BCA (задача требует доказать, что он равен углу ADB)
2) угол BAC (дополнение к углу BAD)
3) угол BCA (дополнение к углу ABC)

Окей, теперь выпишем все факты, которые мы имеем:

1) У нас дано, что угол DAB равен углу ABC.
2) У нас дано, что AK равно KB.

Мы хотим доказать, что угол ADB равен углу BCA.

Теперь давайте рассмотрим, как мы можем доказать это.

Мы знаем, что если два угла одного треугольника равны двум углам другого треугольника, то треугольники подобны.

В нашем случае, у нас есть следующее:

1) угол ADB равен углу ABD, так как эти углы лежат на одной прямой AD
2) угол ADB равен углу BAD, так как угол DAB равен углу ABC, и поэтому угол BAD задается как дополнение к углу ABC, а угол ADB - как дополнение к углу DAB
3) угол BCA равен углу BAC, так как угол DAB равен углу ABC, и поэтому угол BAC - как дополнение к углу BAD, а угол BCA - как дополнение к углу ABC

Таким образом, мы видим, что у нас есть три пары равных углов: (ADB, ABD), (ADB, BAD) и (BCA, BAC).

Исходя из этого, мы можем сделать вывод, что треугольник ADB подобен треугольнику BCA.

А если треугольники подобны, то их углы соответственно равны.

Следовательно, угол ADB равен углу BCA.

Надеюсь, это решение понятно и объясняет, как мы пришли к ответу. Если у вас есть еще вопросы, не стесняйтесь задавать!