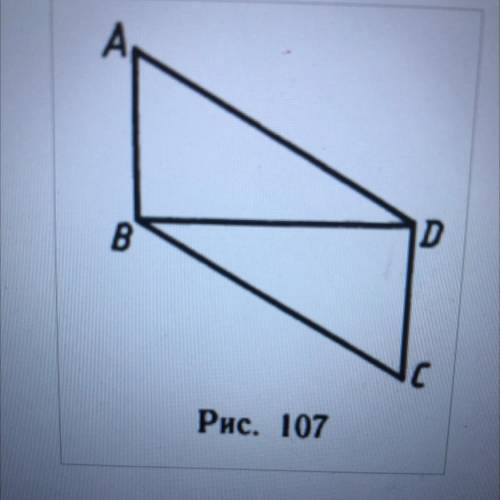
1) На рисунке 107 Угол ABD = углу CDB = 90°, AD=BC. До-
кажите, что AB=CD.

На рисунке 107 дано, что угол ABD равен углу CDB и оба угла равны 90 градусов. Также, дано, что отрезок AD равен отрезку BC. Наша задача - доказать, что отрезок AB равен отрезку CD.

Для начала, мы можем заметить, что угол BDA и угол BCD являются вертикальными. Вертикальные углы равны между собой, поэтому угол BDA = углу BCD.

На основании этого факта и сведений, что углы ABD и CDB равны 90 градусам и угол BDA равен углу BCD, можно сделать вывод, что треугольники ABD и CDB подобны.

Признак подобия треугольников гласит: если два угла в одном треугольнике соответственно равны двум углам в другом треугольнике, то такие треугольники подобны. В нашем случае, углы ABD и CDB равны между собой в обоих треугольниках.

Так как треугольники ABD и CDB подобны, и отрезки AD и BC равны, то отношение длины сторон AD к сторонам AB и AD к CD должно быть одинаковым.

Оформим это равенство отношений с помощью пропорции:

AD/AB = AD/CD

Так как отрезок AD равен отрезку BC, мы можем заменить AD на BC в пропорции:

BC/AB = BC/CD

Затем, мы можем переписать эту пропорцию в виде уравнения:

BC * CD = AB * BC

Теперь мы видим, что BC отменилась на обеих сторонах уравнения:

CD = AB

Таким образом, мы доказали, что отрезок AB равен отрезку CD, что и требовалось доказать.