1.
Известно, что два треугольника подобны: ΔWUS∼ΔKZB.
Не рисуя треугольники, напиши правильное отношение сторон треугольников.

KZ=
KB=
ZB
(в одно окошечко вписывай одну заглавную латинскую букву).

2.
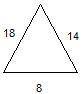
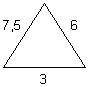
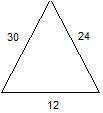
Какой из треугольников не подобен двум другим?

2tr.PNG
3tr.PNG
1trPUSE.PNG
там 3 маленьких треугольника на изображении

3.
Длина отрезка AB равна 12 дм и MN:AB= 9 :1.
Вычисли длину отрезка MN.

ответ: MN=
дм.

4.
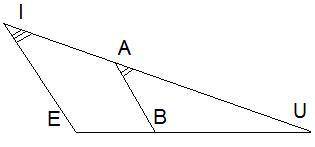
Подобны ли ΔBAUиΔEIU?

Да
Нет

4_platlenkaN2.PNG

5.
tsabs.JPG

Длина тени многоэтажного здания равна 7 м, а длина тени вертикально закреплённого колышка равна 1 м.
Вычисли высоту здания, если высота колышка равна 0,9 м.

ответ: высота здания равна
м.

6.
platlenkaSTU.PNG

Известно, что ΔVTU подобен ΔZSU и коэффициент подобия k= 0,5.
1. Если US= 44, то UT=
.

2. Если VU= 17, то ZU=
.

7.
Площадь треугольника на 78 см2 больше площади подобного треугольника.
Периметр меньшего треугольника относится к периметру большего треугольника как 6 : 7.
Определи площадь меньшего из подобных треугольников.

ответ: S=
см2.

8.
Дано, что BD — биссектриса угла CBA. BA⊥DAиEC⊥BC.

Найди BC, если DA= 9 см, BA= 12 см, EC= 7,2 см.

lidzTr_bis.PNG

Сначала докажем подобие треугольников. (В каждое окошечко впиши одну латинскую букву или число.)

∢
=∢C=
°∢C
E=∢D
A,т.к.BE− биссектриса}⇒ΔCEB∼ΔADB, по двум углам (по первому признаку подобия треугольников).

BC=
см.

9.
Дано: ΔBED∼ΔBCA,
CB= 48, ED= 4, AC= 16.
Найти: BE=
.

trijstABCtaisnED.PNG

twinnyXD    2   18.03.2021 18:57    6