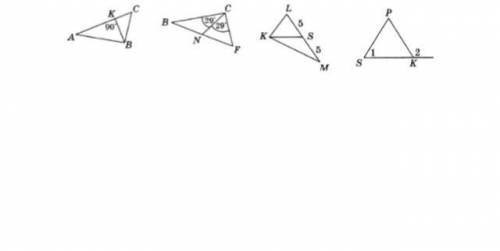
№ 1. Используя рисунок 1, укажите верные утверждения, объясняя почему: 2) ВК – высота треугольника АВС.
3) CN – медиана треугольника BCF.
4) CN – биссектриса треугольника BCF.
5) KS – биссектриса треугольника KLM
Другие вопросы по теме Геометрия
Популярные вопросы
- Розв язати рівняння 1)9х+3=33+3х...
2 - Fill in the preposition (встав пропущений прийменник) 1. Restaurants...
1 - Назвіть характерні риси романтизму. Оберіть три відповіді: 1 заперечення...
2 - іть будь ласка. завдання на фотці!...
2 - Очень Установіть відповідність між безсполучниковими складними реченнями...
1 - 18. Закінчити рівняння реакцій, розставити коефіцієнти: H2SO4 + Al(OH)3...
3 - Напишіть іншу назву голонасінних рослин...
3 - Практическая работа 2 Решение задач по теме Оптика и Электродинамика...
1 - 1. ( ) Спишите предложения, расставьте знаки препинания, где это необходимо....
1 - По похилій площині піднімають вантаж масою 55 кг, прикладаючи до нього...
2
2) Утверждение "ВК – высота треугольника АВС" является верным. Высота треугольника это отрезок, проведенный из вершины треугольника перпендикулярно противоположной стороне. В данном случае, отрезок ВК является перпендикулярным к стороне АВ и проходит через вершину С. Поэтому в АВК получаем прямой угол.
3) Утверждение "CN – медиана треугольника BCF" является верным. Медиана треугольника это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае, отрезок CN соединяет вершину B треугольника BCF с серединой стороны FC.
4) Утверждение "CN – биссектриса треугольника BCF" является неверным. Биссектриса треугольника это отрезок, который делит внутренний угол треугольника на два равных угла. В данном случае, отрезок CN не делит внутренний угол треугольника BCF пополам, поэтому CN не является биссектрисой.
5) Утверждение "KS – биссектриса треугольника KLM" является верным. Подобно объяснению для третьего утверждения, KS является отрезком, который делит внутренний угол треугольника KLM пополам, поэтому KS является биссектрисой.