1. егер үлкен дөңгелектің ауданы 16π см² ал кіші дөңгелектің ауданы π см² болса онда a кесіндінің ұзындығы қандай
2.
егер келесі сандар белгілі бір заңдылықпен орналасса онда y – x айырмасын табыңыз: 4, 6, 10, 18, 34, x, 130, y; болса
3.
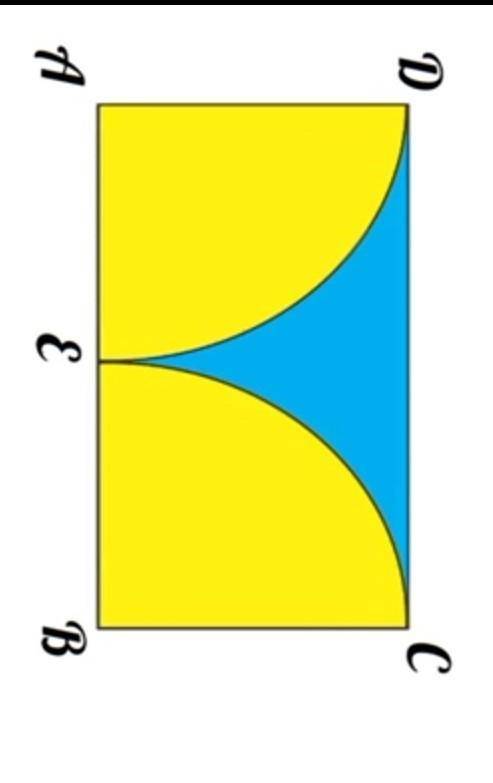
егер AE=BE=AD= 6см. болса
онда боялған бөліктің ауданы қандай болады? (сурет үстінде тұр)
Другие вопросы по теме Геометрия
Популярные вопросы
- Задание: Вставь вместо черточки нужное 1) Имя существительное, имя прилагательное,...
3 - Найди в предложениях союзы и распредели их в колонки. Части составных (повторяющихся)...
3 - 7(x-2)=x-2 знайти корінь будь ласка...
1 - Знания о физической культуре. Гимнастика Выполни задания. 1 Выбери верный ответ....
1 - Хлор в природе существует в виде нуклидов 35 и 37. Рассчитай относительные молекулярные...
2 - 5. Скрестили две сорта кукурузы с длиной початков 20 и 8 см соответственно. Если...
3 - Пажее я не хочу читать это все по произведению островского...
3 - После смерти своей матери (1) Павел отменил отправку военного корпуса во (2) для...
1 - решить задачи по математике N 989; 987; № 994, 995...
2 - В столовой разложили 30 булочек по 6 штук на каждую тарелку. Сколько потребовалось...
1
16π см² = π см² + a см²
а = 16π см² - π см²
а = (16 - 1)π см²
а = 15π см²
Сондықтан, а кесіндінің ұзындығы 15π см².
2. Бізге белгілі бір заңдылық берілбейді, сондықтан бұл сандарды табу мүмкіндігі тартыпты:
4 - 6 = -2
6 - 10 = -4
10 - 18 = -8
18 - 34 = -16
34 - x = -(x - 34)
x - 130 = -(130 - x)
130 - y = -(y - 130)
Осы формулалар арқылы біз "y - x" айырмасын табуға мүмкіндік бар:
4 - 6 = -2
6 - 10 = -4
10 - 18 = -8
18 - 34 = -16
Сондықтан, y - x айырмасын таңдалған сандарда табу мүмкін емес, бірақ жауапты алуға аумақ тартып отырамыз.
3. Суретке қарай, AE = BE = AD = 6 см.
Алайда, CDE үшбұрышының ауданын табу үшін, мына формуланы енгіземіз:
CDE ауданы = AD * CE * sin(ACD)
Кейбір ұтыс сыныптарынан алған білімге басып, ACD бұрышынын енігін анықтау мүмкін:
ACD бұрышының ені = 180° - CEADB бұрышының ені - CED бұрышының ені
CEADB бұрышының ені = 90° (өйткені өзара мекендесетін сияқты көрінеді)
CED бұрышының ені = 60° (өйткені CDE түріндегі барынша бұрышында тең көрінеді)
ACD бұрышының ені = 180° - 90° - 60° = 30°
Сондықтан, CDE ауданы = 6 см * CE * sin(30°)
CE = 2 * CD (Екі сторадан бір түрде бөліп алады)
Осынау CE = 2 * 6 см = 12 см
Сондықтан, CDE ауданы = 6 см * 12 см * sin(30°)
CDE ауданы = 6 см * 12 см * 0.5
CDE ауданы = 36 см²
Олар сұрау жасауды көтеріп, жауаптармен бірге өтетін суретті ұстап күтеміз.