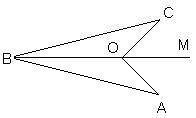
1.Дано:
<АОМ = <СОМ
АО=СО
Доказать: АВ=СВ

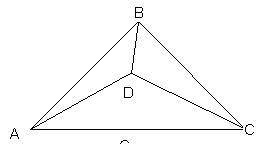
2.Дано:
ВD - биссектриса<АВС
<АDВ = <СDВ
Доказать:∆ АDС – равнобедренный

1 рисунок по 1 номеру,а 2 по 2 номеру

1. Дано:
<АОМ = <СОМ
АО = СО
Доказать: АВ = СВ


Для доказательства равенства АВ = СВ, нам нужно использовать данные, которые даны. Изначально у нас есть два угла, <АОМ и <СОМ, которые равны. И мы знаем, что отрезки АО и СО равны. Нам нужно доказать, что отрезки АВ и СВ также равны.

1. Воспользуемся утверждением, что угол, который стоит на равных отрезках, равен самому себе. Значит, <АОВ = <СОВ.

2. Далее, воспользуемся утверждением, что сумма углов треугольника равна 180 градусов. Получается, что <АОВ + <ВОС + <АВС = 180.

3. Также у нас есть угол между касательной и хордой (в секторе), <АВС. Значит, <АВС = <АОВ + <ВОС.

4. Теперь мы можем заменить <АВС в уравнении 2 на <АОВ + <ВОС. Получаем, что <АОВ + <ВОС + <АОВ + <ВОС = 180.

5. Сокращаем слагаемые: 2<АОВ + 2<ВОС = 180.

6. Делим обе части уравнения на 2: <АОВ + <ВОС = 90.

7. Нам нужно доказать, что отрезки АВ и СВ равны, поэтому нам нужно доказать, что треугольники АВО и СВО равнобедренные. Для этого нам нужно показать, что у них равны боковые стороны и боковые углы.

8. У нас уже есть равные углы <АОВ и <ВОС. Осталось только доказать равенство боковых сторон.

9. Изначально у нас дано, что АО = СО. Нам нужно доказать, что АВ = СВ.

10. Вспомним, что у нас было равенство углов <АОВ = <СОВ. Это значит, что у нас есть две равные стороны и равный угол между ними (по теореме угол-сторона-угол).

11. Таким образом, АВ = СВ, что и требовалось доказать.

Итак, мы доказали, что АВ = СВ, используя данные условия и основные геометрические теоремы.