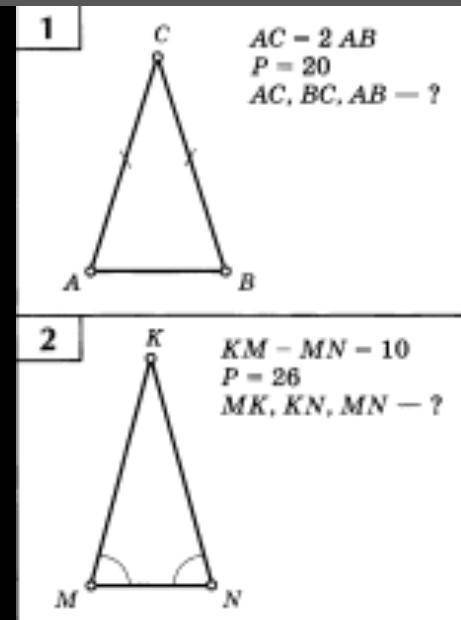
1.Дано: AC=2 AB, P=20

Найти: AC, BC, AB

Решение: (решение самой задачи)

2.Дано: KM-MN-10, P=26

Найти: MK, KN, MN

Решение: (решение самой задачи)

1 - ав = 4см, ас = 8см, вс = 8 см. 2 -

Объяснение:

1.

ас = св, значит св = 2 ав. 2 ав + 2 ав + 1 ав = 5 ав, р = сумма всех сторон, следовательно 20 : 5 = 4, ав = 4, а св = 4 * 2 = 8, ас = 8.

2.

мкн - равнобедренный, значит км = кн, кн - мн = 10, мн = (26 - (10 + 10)) : 3 = 2, следовательно кн = 2 + 10 = 12, мн = 12.

по-моему так)

1. Решение первой задачи:

Дано: AC = 2AB, P = 20

Для начала, нам необходимо понять, какие величины представляют собой AC, BC и AB.

AC - это отрезок, который соединяет точку A с точкой C.
BC - это отрезок, который соединяет точку B с точкой C.
AB - это отрезок, который соединяет точку A с точкой B.

Зная, что AC = 2AB, мы можем переписать уравнение следующим образом:
AB + BC = 2AB

Разделим оба выражения на AB:
BC/AB + 1 = 2

Теперь, чтобы найти AC, мы можем записать уравнение следующим образом:
AC = AB + BC

Так как у нас уже есть соотношение BC/AB + 1 = 2, мы можем подставить это в уравнение для AC:
AC = AB + (BC/AB + 1)*AB
AC = AB + BC + AB
AC = 2AB + BC

У нас также есть информация, что P = 20. P - это периметр треугольника, то есть сумма всех сторон треугольника. Мы можем записать уравнение для P:
P = AC + BC + AB

Подставив значения из уравнения для AC выше, мы получим:
20 = 2AB + BC + AB

Теперь, когда у нас есть два уравнения:
BC/AB + 1 = 2
20 = 2AB + BC + AB

Мы можем решить эту систему уравнений, чтобы найти значения AC, BC и AB.

2. Решение второй задачи:

Дано: KM - MN = 10, P = 26

Как и в предыдущей задаче, нам необходимо понять, что представляют собой величины KM, KN и MN.

KM - это отрезок, который соединяет точку K с точкой M.
KN - это отрезок, который соединяет точку K с точкой N.
MN - это отрезок, который соединяет точку M с точкой N.

Зная, что KM - MN = 10, мы можем записать это уравнение следующим образом:
KM = MN + 10

У нас также есть информация, что P = 26. P - это периметр треугольника KNM, то есть сумма всех его сторон. Мы можем записать уравнение для P:
P = KM + KN + MN

Подставив значение KM из уравнения KM = MN + 10, мы получим:
26 = MN + 10 + KN + MN

Теперь, когда у нас есть уравнение:
26 = 2MN + KN + 10

Мы можем решить это уравнение, чтобы найти значения MK, KN и MN.