1) Дана трапеция ABCD с основаниями BC= 5 см и AD= 10 см. Высота BE проведена к основанию AD и равна 4 см.
Вычисли площадь трапеции.
2)
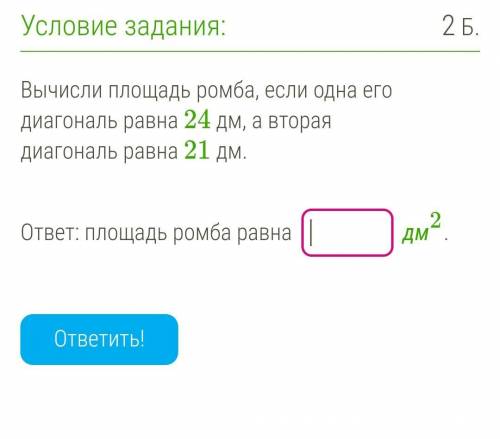
Вычисли площадь ромба, если одна его диагональ равна 24 дм, а вторая диагональ равна 21 дм
3)
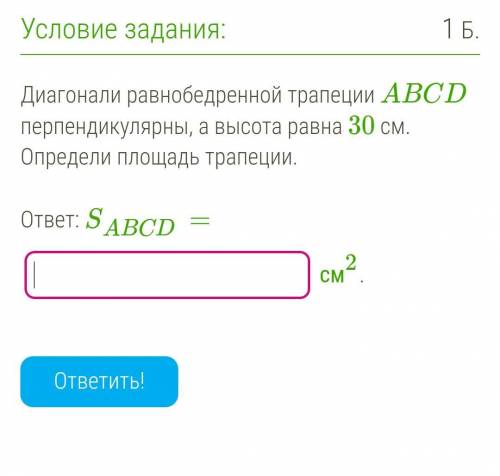
Диагонали равнобедренной трапеции ABCD перпендикулярны, а высота равна 30 см. Определи площадь трапеции.
ответ: SABCD=
4)
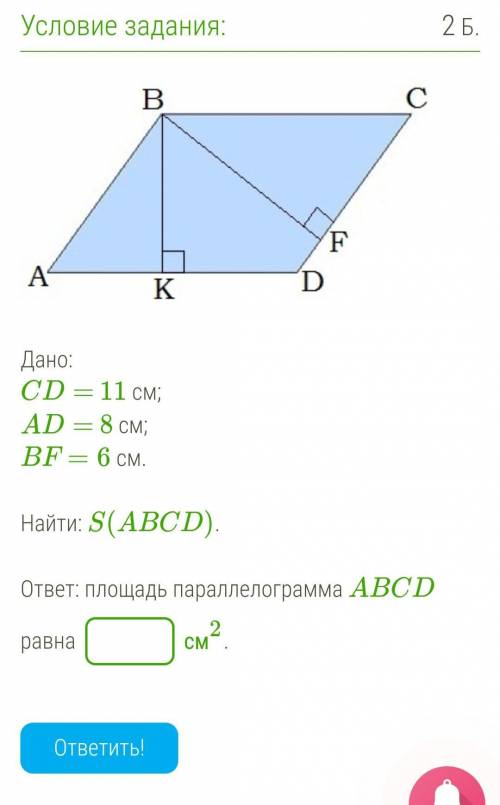
Дано:
CD= 11 см;
AD= 8 см;
BF=6 см.
Найти: S(ABCD).
ответ: площадь параллелограмма ABCD равна
5)
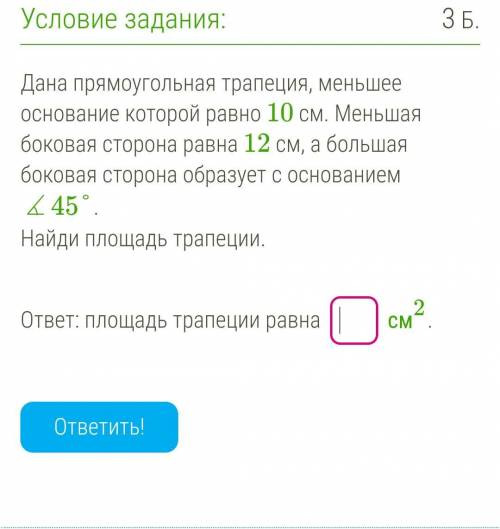
Дана прямоугольная трапеция, меньшее основание которой равно 10 см. Меньшая боковая сторона равна 12 см, а большая боковая сторона образует с основанием ∡45°.
Найди площадь трапеции.
6)
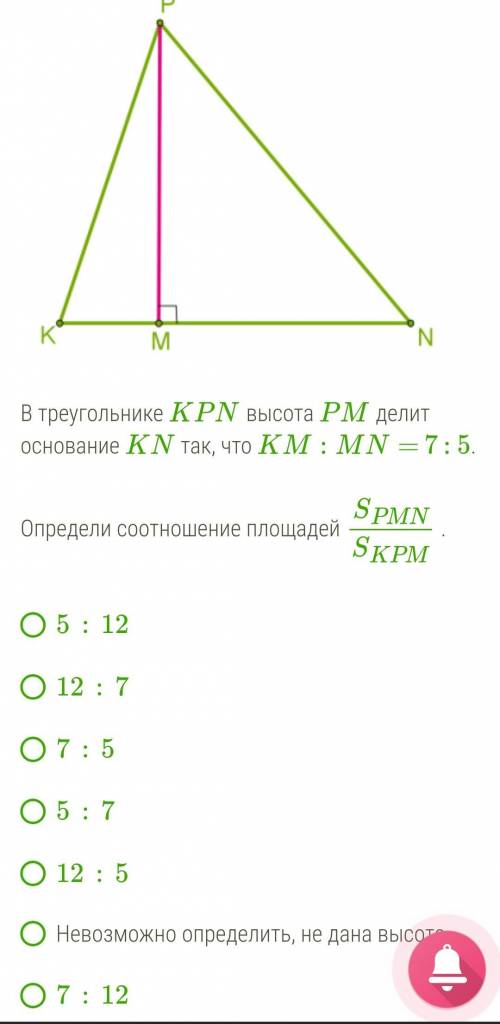
В треугольнике KPN высота PM делит основание KN так, что KM:MN= 7 : 5.
Определи соотношение площадей SPMNSKPM .
5:12
12:7
7:5
5:7
12:5
Невозможно определить, не дана высота
7:12
Другие вопросы по теме Геометрия
Популярные вопросы
- Почему в период дворцовых переворотов в россии было много иностранцев(особенно...
2 - Что означает выражение: спартанка вручая сыну щит говорила или с ним,сын мой,...
3 - Перевести с на текст используя презент перфект в эти выходные я ходила в тематический...
1 - 14 целых 5/8 + (5целых 3/8- 4целых 7/8) пляз нужно...
2 - Идея, тема, основная мысли и стих а.а. фет первый ландыш? ?...
1 - Выражения и найдите его значение при в = 3 четырнадцать семнадцатых 1)-9,72+в+7,4+5,72+(-7,4)=...
3 - Надо выразить c c= вот и сам пример a+w-d+c-e+f=g+i-h...
3 - Решите уравнение x + 14 6x+1 _ =1 5 7...
2 - 1)найдите число,если 25,6% этого числа-это 16/23 числа4,6 2)что больше 30% от...
2 - Сочинение 10 предложений на тему интересная профессия...
1
S = ((a + b) * h) / 2,
где a и b - основания трапеции, h - высота.
В данном случае основания BC = 5 см и AD = 10 см, а высота BE = 4 см. Подставляем значения в формулу:
S = ((5 + 10) * 4) / 2 = (15 * 4) / 2 = 60 / 2 = 30 см^2.
Ответ: Площадь трапеции равна 30 см^2.
2) Для вычисления площади ромба можно использовать формулу:
S = (d1 * d2) / 2,
где d1 и d2 - диагонали ромба.
В данном случае одна диагональ равна 24 дм, а вторая диагональ равна 21 дм. Подставляем значения в формулу:
S = (24 * 21) / 2 = 504 / 2 = 252 дм^2.
Ответ: Площадь ромба равна 252 дм^2.
3) В данном случае диагонали равнобедренной трапеции перпендикулярны и высота равна 30 см. Площадь трапеции можно найти, используя формулу:
S = ((a + b) * h) / 2,
где a и b - основания трапеции, h - высота.
В данном случае диагонали равны и высота равна 30 см. Подставляем значения в формулу:
S = ((a + a) * 30) / 2 = (2a * 30) / 2 = 60a / 2 = 30a.
Ответ: Площадь трапеции равна 30a квадратных сантиметров.
4) Для вычисления площади параллелограмма ABCD можно использовать формулу:
S = a * h,
где a - основание параллелограмма, h - высота.
В данном случае CD = 11 см, AD = 8 см и BF = 6 см. Площадь параллелограмма можно найти, используя формулу:
S = CD * AD = 11 * 8 = 88 см^2.
Ответ: Площадь параллелограмма ABCD равна 88 см^2.
5) Для вычисления площади трапеции можно использовать формулу:
S = ((a + b) * h) / 2,
где a и b - основания трапеции, h - высота.
В данном случае меньшее основание равно 10 см, меньшая боковая сторона равна 12 см, а большая боковая сторона образует с основанием ∡45°. Поскольку мы не знаем, как конкретно образуются углы между боковыми сторонами и основанием, невозможно определить конкретную высоту или площадь трапеции. Поэтому нам не хватает информации для решения этой задачи.
Ответ: Невозможно определить площадь трапеции без дополнительной информации.
6) Обозначим длину основания KN как x. Поскольку высота PM делит основание KN так, что KM:MN = 7:5, то KM = (7x) / (7+5) = (7x) / 12 и MN = (5x) / (7+5) = (5x) / 12. Тогда соотношение площадей SPNM и SKPM можно выразить следующим образом:
SPNM:SKPM = (1/2 * PM * MN) : (1/2 * PM * KM) = (1/2 * x * (5x/12)) : (1/2 * x * (7x/12)) = (5x^2/24) : (7x^2/24) = 5x^2 : 7x^2 = 5 : 7.
Ответ: Соотношение площадей SPMNSKPM равно 5:7.