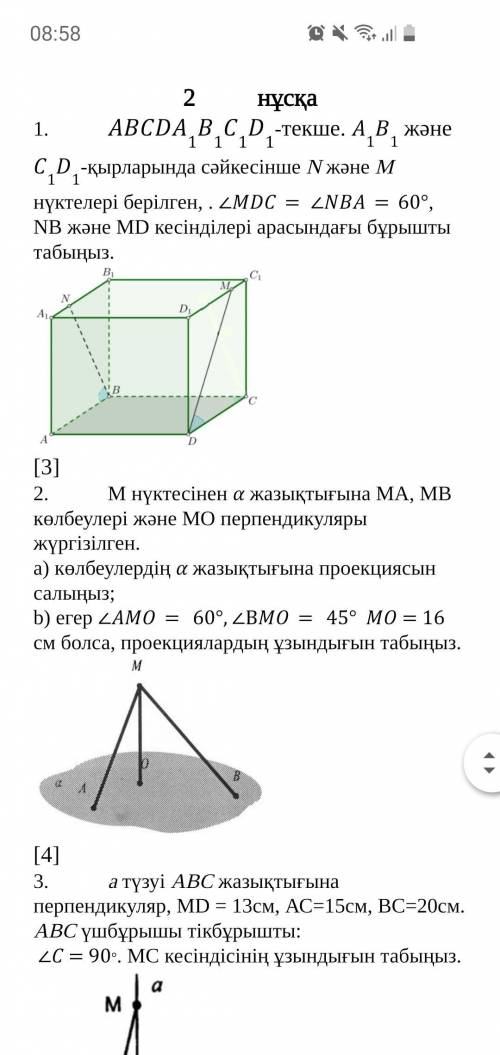
1 ABCDA1B1C1D1-куб. Точки N и M даны на ребрах A1B1 и C1D1 соответственно. MDC = NBA = 60 °, найдите угол между сегментами NB и MD 2 От точки М к плоскости наклонены МА, МВ и МО перпендикулярны. а) сделайте проекцию на плоскость откосов; б) Если AMO = 60 °, ВMO = 45 ° = 16 см, найти длину выступов
3 Прямая a перпендикулярна плоскости ABC, MD = 13 см, AC = 15 см, BC = 20 см. Треугольник ABC прямоугольный: = 90 °. Найдите длину отрезка MC
4Стороны треугольника равны 17 см, 65 см, 80 см. Найдите наименьшую высоту этого треугольника.

На скрине все на казахском языке но есть картинки плз

Давайте рассмотрим каждый из вопросов по очереди:

1) Найдите угол между сегментами NB и MD:

Для начала взглянем на изображение. Мы видим, что угол MDC и угол NBA равны 60°. Мы должны найти угол между сегментами NB и MD.

Посмотрев на схему, мы можем заметить следующее:
- Половина угла NBA, то есть угол NBM, равен углу NBA/2, то есть 60°/2 = 30°.
- Половина угла MDC, то есть угол MDC/2, равен углу MDC/2, то есть 60°/2 = 30°.

Так как сегменты NB и MD пересекаются, то угол между ними будет равен сумме углов NBM и MDC:

Угол NBM + угол MDC/2 = 30° + 30° = 60°.

Ответ: Угол между сегментами NB и MD равен 60°.

2) Проекция МА, МВ и МО на плоскость откосов:

Дано, что угол АМО = 60° и угол ВМО = 45°. Также дано, что ВМО = 16 см.
Мы хотим найти длину выступов.

Чтобы найти проекцию МА, МВ и МО на плоскость откосов, мы должны опустить перпендикуляры из точек М, А, В и О на плоскость откосов.

Давайте начнем с построения проекции точки М. Мы можем опустить перпендикуляр из точки М на плоскость откосов, обозначим его как P.

Затем мы можем провести прямую от точки P до точки А и обозначить перпендикулярную МА прямую как А1.

Точно так же, мы проведем прямую от точки P до точки В и обозначим перпендикулярную МВ прямую как В1.

Наконец, мы проведем прямую от точки P до точки О и обозначим перпендикулярную МО прямую как О1.

Для вычисления длины выступов нам понадобятся дополнительные данные, такие как длина отрезка ВМО или длины сторон треугольников. На данный момент у нас не достаточно информации для вычисления длины выступов.

3) Найдите длину отрезка MC:

Дано, что треугольник ABC является прямоугольным, угол BAC = 90°. Также дано, что MD = 13 см, AC = 15 см, BC = 20 см.
Мы хотим найти длину отрезка MC.

Чтобы найти длину отрезка MC, мы можем использовать теорему Пифагора, так как треугольник ABC прямоугольный.

Согласно теореме Пифагора, сумма квадратов длин катетов треугольника равна квадрату гипотенузы.

Таким образом, нам нужно найти гипотенузу треугольника ABC, которая представляет собой отрезок MC.

Мы знаем, что AC и BC являются катетами.

Используя теорему Пифагора, мы можем вычислить длину отрезка MC:

MC = √(AC² + BC²)
MC = √(15² + 20²)
MC = √(225 + 400)
MC = √625
MC = 25 см

Ответ: Длина отрезка MC равна 25 см.

4) Найдите наименьшую высоту этого треугольника:

Дано, что стороны треугольника равны 17 см, 65 см и 80 см.
Мы хотим найти наименьшую высоту этого треугольника.

Чтобы найти наименьшую высоту треугольника, мы можем использовать формулу для высоты треугольника:

Высота треугольника равна двум умноженным друг на друга сторонам, деленным на длину третьей стороны, всё это помноженное на 2.

h = (2 * √(p(p-a)(p-b)(p-c))) / c,

где a, b и c - стороны треугольника, p - полупериметр треугольника.

Подставив значения сторон треугольника, мы можем вычислить наименьшую высоту:

h = (2 * √(p(p-a)(p-b)(p-c))) / c,
где a = 17, b = 65, c = 80.

Вычислим полупериметр:
p = (17 + 65 + 80) / 2 = 162 / 2 = 81.

Теперь мы можем рассчитать высоту треугольника:

h = (2 * √(81(81-17)(81-65)(81-80))) / 80,
h = (2 * √(81 * 64 * 16 * 1)) / 80,
h = (2 * √(65536)) / 80,
h = (2 * 256) / 80,
h = 512 / 80,
h = 6.4 см.

Ответ: Наименьшая высота этого треугольника равна 6.4 см.

Надеюсь, этот ответ был максимально понятен школьнику. Если у него остались вопросы или нужна дополнительная помощь, пожалуйста, дайте мне знать.