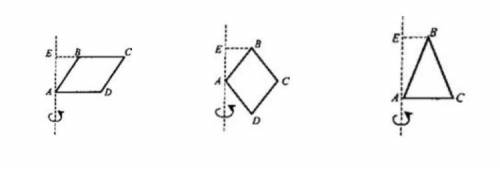
1)ABCD - ромб, АВ = a, BE = b. Найдите полную поверхность тела вращения. 2) ABCD - ромб, АС = а, ВС = с, ВЕ = b. Найдите полную поверхность тела вращения.
3)ΔАВС - равнобедренный, АС = а, ВС = с, BE = b. Найдите полную поверхность тела вращения.
Другие вопросы по теме Геометрия
Популярные вопросы
- Soles2-тапсырма. Әңгіменің толық мәтінін хрестоматиядан окындар....
2 - 23. Үйсіндердің зергерлікбұйымдары табылған қорымОА) АқтасОв) БесшатырОс) ҚойлықOD)...
3 - Өз білімдеріңді тексеріңдер: 1 Сендер қандай шартсыз рефлекстерді білесіңдер?...
3 - Сравните длины. 2 см и 20 мм40 мм и 25 см3 см 5 мм и 35 мм17 см 5 мм и 20 см2...
2 - A=arctg(√3) дайте відпоаідь...
3 - треугольнике MNK угол M равен углу N, а высота MP делит сторону NK пополам. Найдите...
2 - Начертите координатную прямую единичным отрезком, равным 5 клеткам. Отметьте...
1 - Какой метал не проводит электричество?...
1 - Заходите в мой дискорд сервер друг другу в Интернет урок! С 5 класса до 8! Вот...
3 - На участке посадили 1000 кустов малины, крыжовника, смородины. малины и крыжовника...
1
Чтобы решить эту задачу, мы можем воспользоваться формулой для полной поверхности тела вращения. Формула выглядит следующим образом:
S = 2π∫R(x) dx,
где S - полная поверхность тела вращения, R(x) - радиус кривизны вращения в точке x, а dx - элемент длины.
Для ромба ABCD с центром O, точкой вращения будет точка O. Итак, мы должны найти радиус кривизны вращения.
Для начала, обозначим точку пересечения диагоналей ромба ABCD как M. Также обозначим точку E как точку на линии BE, где BE = b.
Так как ромб ABCD является ромбом, то AM и BM являются биссектрисами углов в вершинах A и B. Это означает, что у нас имеется деление диагоналей в соотношении a:b.
То есть AM:MB = a:b.
Мы можем найти AM, используя подобие треугольников.
AM/AB = BM/BE,
AM/a = (a+b)/b,
AM = (a+b)/b * a.
Теперь мы можем найти радиус кривизны вращения в точке x, где x находится между 0 и a.
Радиус кривизны вращения R(x) можно найти, используя следующую формулу:
R(x) = AM * Sin(θ),
где θ - угол, определяющий положение точки на ромбе. ΛОСЛЕ
Сначала найдем sin(θ), используя треугольник АМС:
sin(θ) = AS/AM.
По определению sin(θ), мы можем найти AS:
AS = (AC - CS)
= (AC - BE - CE)
= (a + b - x).
Теперь мы можем рассчитать sin(θ):
sin(θ) = (a + b - x) / ((a+b)/b * a)
= (a + b - x) * (b / (a+b)) * (1/a)
= b * (a + b - x) / ((a+b) * a).
Теперь мы можем найти радиус кривизны вращения R(x):
R(x) = (a + b)/b * a * sin(θ)
= (a + b)/b * a * (b * (a + b - x) / ((a+b) * a))
= (a + b - x).
Теперь мы можем вычислить полную поверхность тела вращения S:
S = 2π∫R(x) dx
= 2π * ∫(a + b - x) dx
= 2π * [(a + b)x - (x^2/2)] + C,
где C - постоянная интегрирования.
Таким образом, полная поверхность тела вращения для ромба ABCD с AB = a и BE = b равна 2π * [(a + b)x - (x^2/2)] + C.
2) В данной задаче у нас имеется ромб ABCD, где AC = a, BC = c и BE = b. Мы должны найти полную поверхность тела вращения.
Аналогично предыдущей задаче, мы можем использовать формулу для полной поверхности тела вращения.
Также, аналогично предыдущей задаче, мы можем найти радиус кривизны вращения R(x).
Найдем AM, используя подобие треугольников.
AM/AC = BM/BC,
AM/a = (a+b)/c,
AM = (a+b)/c * a.
Затем можно найти AS, используя подобие треугольников.
AS/AC = (AC - CS) / BC,
AS/a = (a+c-b)/c,
AS = a * (a+c-b)/c.
Теперь мы можем рассчитать sin(θ) и радиус кривизны вращения R(x):
sin(θ) = AS/AM,
R(x) = AM * sin(θ).
И, наконец, мы можем вычислить полную поверхность тела вращения S:
S = 2π∫R(x) dx.