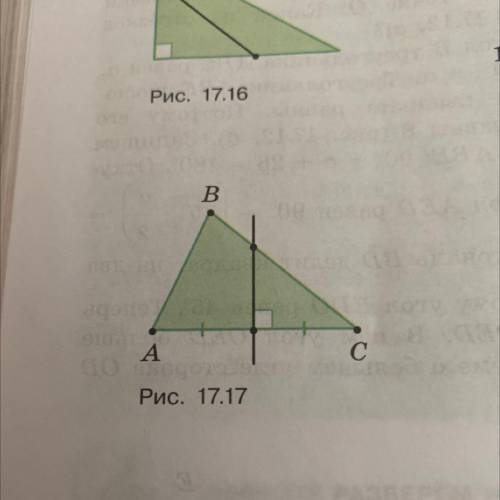
1.6 * Серединный перпендикуляр к стороне Ас
треугольника ABC пересекает его
сторону BC.
Докажите, что ВС > AB (рис. 17.17).

Для того чтобы доказать, что BC > AB, нам нужно рассмотреть серединный перпендикуляр к стороне Ас треугольника ABC, пересекающий его сторону BC.

Чтобы начать доказательство, давайте вспомним некоторые основные понятия о треугольниках.

- Серединный перпендикуляр к отрезку AB - это отрезок, перпендикулярный AB и проходящий через его середину. В данном случае, серединный перпендикуляр к стороне Ас будет перпендикулярным к BC и будет проходить через середину стороны Ас.

Теперь, давайте обратимся к изображению. Для обозначений, давайте назовем точку пересечения серединного перпендикуляра с стороной BC как D.

Таким образом, у нас есть следующие известные условия:
- AD = DC (по определению серединного перпендикуляра)
- Серединный перпендикуляр AD встречается с BC в точке D.

Теперь мы можем приступить к доказательству неравенства BC > AB. Для этого мы воспользуемся неравенством треугольника, которое утверждает, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.

В нашем случае, мы можем рассмотреть треугольники ABD и BCD. Известно, что AD = DC, а также мы знаем, что AD + DB > AB и DC + DB > BC (по неравенству треугольника).

Учитывая, что AD = DC и сочетая эти два неравенства, мы получаем следующее:
AD + DB = DC + DB > AB + BC

Из этого неравенства мы можем заключить, что BC > AB, так как AB + BC < AD + DB.

Таким образом, мы доказали, что BC > AB, используя теорию треугольников и неравенство треугольника.