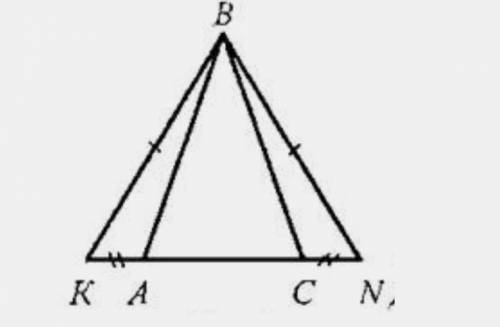
Дано:
BK=BN
AK=CN
Доказать:
∆ABC – равнобедренный,.

​

Для доказательства того, что треугольник ABC является равнобедренным, мы должны показать, что две стороны треугольника равны. Из условий задачи дано, что BK = BN и AK = CN. Мы знаем, что BK = BN, поэтому можно сделать вывод, что у отрезков BK и BN равны длины. Также известно, что AK = CN, что значит, что у отрезков AK и CN также равны длины. Теперь мы можем рассмотреть треугольники ABK и ACN. У этих треугольников две стороны равны, так как BK = BN и AK = CN. Таким образом, по правилу равнобедренности треугольников, мы можем сделать вывод, что углы при основаниях этих треугольников (то есть углы B и C) равны. Теперь мы должны доказать, что угол A также равен углам B и C. Мы можем воспользоваться следующим фактом: сумма углов в треугольнике равна 180 градусам. В треугольнике ABC сумма углов A, B и C равна 180 градусам. Поскольку углы B и C равны между собой (мы доказали это ранее), то можем записать следующее уравнение: A + B + C = 180. Теперь мы можем заменить B и C на их равные значения (углы при основании ABK и ACN) и получить следующее уравнение: A + (угол при основании ABK) + (угол при основании ACN) = 180. Но угол при основании ABK и угол при основании ACN равны, поскольку треугольники ABK и ACN равнобедренные. Поэтому мы можем записать уравнение в следующем виде: A + B + B = 180. Теперь мы можем объединить углы B и B и записать уравнение в следующем виде: A + 2B = 180. Чтобы доказать, что угол A равен углу B, мы можем решить это уравнение относительно A: A = 180 - 2B. Теперь мы знаем, что углы A и B в треугольнике ABC равны, что делает треугольник равнобедренным. Таким образом, условие "∆ABC – равнобедренный" доказано.