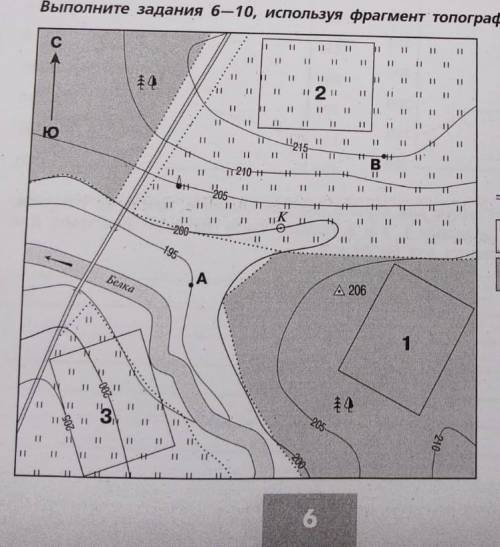
7. определите расстояние по прямой от башни до геодезического знака. результат округлите до десятков метров. ответ запишите в виде числа )

Для решения данной задачи, нам необходимо использовать теорему Пифагора. Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Гипотенузой называется сторона треугольника, противолежащая прямому углу, а катеты - остальные две стороны. В данной задаче, башня является основанием треугольника, геодезический знак - вершиной, а расстояние между ними - гипотенузой. По условию задачи, известны значения катетов. Теперь приступим к решению: Шаг 1: Запишем данные из условия задачи: Катет AB (высота башни) = 45 м. Катет BC (горизонтальное расстояние от башни до геодезического знака) = 60 м. Шаг 2: Применим теорему Пифагора: H^2 = AB^2 + BC^2 Шаг 3: Подставим известные значения: H^2 = 45^2 + 60^2 Шаг 4: Выполним вычисления: H^2 = 2025 + 3600 H^2 = 5625 Шаг 5: Извлечем квадратный корень для нахождения значения гипотенузы: H = √5625 H = 75 метров Шаг 6: Округлим результат до десятков метров: Ответ: 70 метров. Таким образом, расстояние по прямой от башни до геодезического знака составляет 70 метров (округлено до десятков метров).