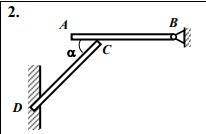
Знатокам привет. Однородная балка АВ длиной 4 м и весом 2 кН
шарнирно прикреплена к неподвижной опоре В, а промежуточной точкой опирается на балку СD длиной 3 м и
весом 2 кН, которая жёстко заделана в стену. Определить
реакции в точках D, С и В, если угол = 30 градусов, АС = 1 м.
Составить проверку

Привет! Для того чтобы решить эту задачу, мы можем использовать условия равновесия механической системы. Когда система находится в равновесии, сумма всех горизонтальных сил, вертикальных сил и моментов должна быть равной нулю.

Давайте рассмотрим каждую величину по отдельности. Сначала найдем горизонтальные силы. Из условия равновесия можно сказать, что сумма всех горизонтальных сил должна быть равна нулю.

В данной задаче, на горизонтальную ось действуют только усилия реакций опор, которые обозначены RD и RB. Так как система находится в равновесии, то сумма горизонтальных сил должна быть равна нулю:
RD + RB = 0

Теперь рассмотрим вертикальные силы. Из условия равновесия можно сказать, что сумма всех вертикальных сил должна быть равна нулю.

На вертикальную ось действуют веса балок AV и CD, а также реакций опор VB и VC:
VA + VD + VB + VC = 0

Зная, что вес балки AV равен 2 кН и вес балки CD также равен 2 кН, мы можем записать следующее уравнение:
2 + VD + VB + VC = 0

Теперь давайте рассмотрим моменты. В данной задаче, момент силы в каждой точке должен быть равен нулю.

Момент силы приложенной в точке В равен нулю, так как опора В является шарнирной и не создает моментов:
VB * 4 - 2 * 1 = 0

Момент силы, создаваемой весом балки AV, относительно точки D равен нулю:
2 * 4 * cos(30) - VD * 1 = 0

Момент силы, создаваемой весом балки CD, относительно точки C равен нулю:
-2 * 3 * cos(30) - VC * 1 = 0

Теперь у нас есть система уравнений:
RD + RB = 0
VA + VD + VB + VC = 0
VB * 4 - 2 * 1 = 0
2 * 4 * cos(30) - VD * 1 = 0
-2 * 3 * cos(30) - VC * 1 = 0

Мы можем решить эту систему уравнений методом подстановки или методом Крамера, чтобы найти значения реакций в точках D, С и В.

Проверка будет заключаться в том, что величины реакций в точке D, С и В должны соответствовать условию равновесия механической системы. Если сумма горизонтальных сил, вертикальных сил и моментов будет равна нулю, то реакции в точках D, С и В найдены правильно.