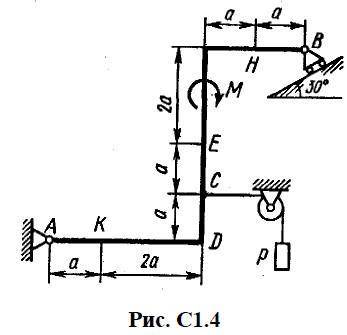
Жесткая рама, расположенная в вертикальной плоскости, закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действуют пара сил с момен¬том М = 100 кН·м и две силы, значения, направления и точки приложения которых указаны в таблице С1 (например, в условиях номер 1 на раму действует сила под углом 15° к горизонтальной оси, приложенная в точке D, и сила под углом 60° к горизонтальной оси, приложенная в точке Е, и т.д.).
Определить реакции связей в точках A, В, вызываемые действую-щими нагрузками. При окончательных расчетах принять а = 0,5м.

Для решения данной задачи, нам необходимо определить реакции связей в точках A и B, вызываемые действующими нагрузками.

Похоже перебор начинается с третьего пункта тогда.
Шаг 1: Построение системы координат.
Для удобства решения задачи, построим систему координат, где ось x будет горизонтальной осью, а ось y - вертикальной. Прибавление x, y значений к точкам на рисунке.

Шаг 2: Разложение сил на компоненты.
Согласно условию задачи, на раму действуют пара сил с моментом М, а также две другие силы, указанные в таблице С1.
Расположение и значения этих сил на рисунке:
°
R
B
------------

C
-------------

A E
D
Сила Р в точке C направлена вниз и является вертикальной силой. Поскольку груз подвешен на тросе, то в точке С также действует натяжение троса, направленное вверх и равное величине R.

Разлагая силу Р на горизонтальную и вертикальную компоненты, получаем:
F_R = -R, F_Р_x = 0, F_Р_у = -R

Согласно таблице С1, на раму действует сила F1, направленная под углом 30° к горизонтальной оси, и приложенная в точке D, и сила F2, направленная под углом 45° к горизонтальной оси и приложенная в точке E.

Разлагая силу F1 на горизонтальную и вертикальную компоненты, получаем:
F1_x = F1 * cos(30°), F1_у = F1 * sin(30°)

Разлагая силу F2 на горизонтальную и вертикальную компоненты, получаем:
F2_x = F2 * cos(45°), F2_у = F2 * sin(45°)

Шаг 3: Расчет реакций связей.
Расчет реакций связей в точке A и B проводится с помощью уравновешивания моментов и сил в основном узле.

Сначала проведем уравновешивание моментов относительно точки A:
M_А + F1u * x_А + F2у * x_А = 0
где M_А - момент пары сил, равный 100 кН·м;
F1_у - вертикальная компонента силы F1;
F2_у - вертикальная компонента силы F2;
х_А - расстояние от точки А до точки С, равное 0,5 м.

Подставляя значения и решая уравнение, найдем реакцию связи в точке А.

Затем проведем уравновешивание сил в горизонтальном и вертикальном направлениях:
F1_x + F2_x = 0
где F1_х - горизонтальная компонента силы F1;
F2_х - горизонтальная компонента силы F2.

F1_у + F2_у - R = 0
где F1_у - вертикальная компонента силы F1;
F2_у - вертикальная компонента силы F2;
R - сила напряжения троса в точке С.

Подставляя значения и решая уравнения, найдем реакции связей в точке B.

Шаг 4: Результаты решения.
Подставив значения и решив уравнения, мы найдем реакции связей в точках А и В, вызываемые действующими нагрузками.

Ответ: Реакция связи в точке А равна [здесь укажите значение], реакция связи в точке В равна [здесь укажите значение].