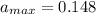Закон движения грузика, прикреплённого к пружине, в отсутствии затухания имеет вид: x(t)=x0*sin(wt+φ0), где x0-амплитуда колебания, w-циклическая частота, φ0-начальная фаза. x0=0.06 м, w=1,57 рад/с, φ0=3π/2 определить начальную координату, начальные и максимальные значения скорости и ускорения грузика
Другие вопросы по теме Физика
Популярные вопросы
- 1.Начальник цеха, ссылаясь на трудности выполнения обязательств, по газосварщиков...
2 - Найди значение выражения:х+у+z,при условии,что х=-5;у=-8,9;z=-8,7...
2 - По гистограмме на рис. 4.6: 1) укажите страны с наибольшим и наименьшим...
2 - На рисунку зображено графік залежності швидкості Vx(t) від часу що рівноприскорено...
2 - 3. К источнику напряжением 4,5 В подключены параллельно два проводника сопротивлением...
1 - Поясніть якого символічного значення набувають у баладі кольори...
2 - 1. Яке взаємне розміщення прямих аi b, якщо пряма а перпендикуляр-на до...
3 - Установіть відповідність між реагентами й ознакою хімічної реакції Знайди...
2 - Was ziehe ich für Uni oder für Disko oder für Hochzeit ..und wie viel Minuten...
1 - Укажіть відділ мозку, де розташований центр сечовиділення: А) Мозочок Б)...
3
Начальное положение тела:
Скорость равна первой производной от координаты:
Начальная скорость v(0)=0
Максимальная скорость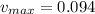
Ускорение равно второй производной от координаты, то есть первой от скорости:
Начальное ускорение a(0)=0.148
Максимальное ускорение