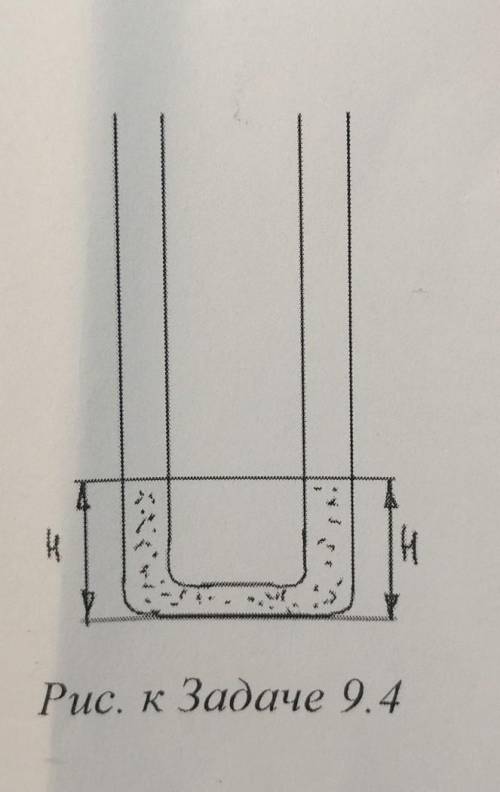
Задача 9.4. В одинаковые высокие сообщающиеся сосуды налита жидкость с плотностью pт. так, что ее высота равна н (рис.) в правый сосуд начинают очень медленно подливать другую, более легкую жидкость с плотностью рл. Постройте график зависимости высоты столба жидкости в левом сосуде от высоты столба более легкой жидкости? Жидкости не перемешиваются. Толщиной соединяющей трубки можно пренебречь. Жидкости из сосудов не выливаются.

Для решения данной задачи, мы можем использовать закон Паскаля, который гласит, что давление, создаваемое на любую точку жидкости, равно во всех направлениях и пропорционально плотности жидкости и ее высоте.

В данном случае мы имеем две жидкости в двух разных сосудах, которые сообщаются между собой через трубку. Сосуды имеют одинаковую высоту и для удобства обозначим ее как h.

Пусть высота столба более легкой жидкости (плотностью рл) в правом сосуде будет равна x. Тогда высота столба жидкости с плотностью pт в левом сосуде будет равна (h - x).

Так как жидкости находятся в состоянии равновесия и не перемешиваются, то давление на всех точках на одной горизонтальной плоскости будет одинаковым.

Давление, создаваемое столбом жидкости с плотностью pт на глубине h-x, равно pт * g * (h - x), где g - ускорение свободного падения.

Давление, создаваемое столбом более легкой жидкости на глубине x, равно рл * g * x.

Из закона Паскаля следует, что эти давления должны быть равными:

pт * g * (h - x) = рл * g * x

Убираем g:

pт * (h - x) = рл * x

Раскрываем скобки:

pт * h - pт * x = рл * x

Переносим всё, что содержит x, на одну сторону уравнения:

pт * h = рл * x + pт * x

Раскрываем скобки:

pт * h = (рл + pт) * x

Делим обе части уравнения на (рл + pт):

x = (pт * h) / (рл + pт)

Таким образом, мы получаем формулу для зависимости высоты столба более легкой жидкости от высоты столба жидкости с плотностью pт:

x = (pт * h) / (рл + pт)

Теперь мы можем построить график зависимости x от h (высоты столба жидкости с плотностью pт). Чтобы это сделать, мы можем задать различные значения для pт и рл, а затем рассчитать значения x при различных значениях h и построить график.

Следует также отметить, что эта формула справедлива только для идеальных условий, когда мы можем пренебречь толщиной соединяющей трубки и расположением сосудов по отношению к горизонтали. В реальности эти факторы также будут влиять на результаты.