Яка з наведених на рисунку деформованих пружин має найменшу потенціальну енергію?С полным решением!

Для ответа на данный вопрос, нам необходимо понять, как связана потенциальная энергия деформированной пружины с ее характеристиками. Потенциальная энергия пружины определяется законом Гука и зависит от ее упругости и изменения ее длины.

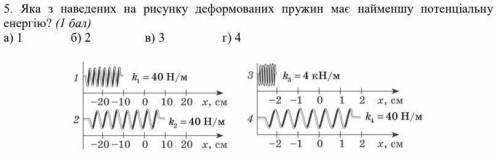
На рисунке представлены четыре пружины с разными степенями деформации. Давайте рассмотрим каждую пружину и определим, какая из них имеет наименьшую потенциальную энергию.

1. Прежде всего, вспомним, что упругая энергия пружины определяется формулой U = (1/2)kx^2, где U - потенциальная энергия пружины, k - коэффициент жесткости пружины и x - изменение ее длины.

2. В первом случае, пружина изображена без деформации, то есть без изменения длины. Такая пружина не хранит упругой энергии, поэтому потенциальная энергия пружины равна нулю.

3. Во втором случае, пружина деформирована постепенно и ее длина увеличена незначительно. Так как изменение длины пружины (x) мало, то и ее потенциальная энергия будет незначительной.

4. В третьем случае, пружина сильно деформирована, а ее длина значительно увеличена. Это изменение длины (x) будет приводить к большему значению потенциальной энергии пружины.

5. В четвертом случае, пружина деформирована, и ее часть сократилась. Если пружина сжата или сокращена, это означает, что ее длина (x) отрицательна. Изменение знака в формуле для потенциальной энергии (U = (1/2)kx^2) приведет к положительному значению потенциальной энергии пружины.

Исходя из вышесказанного, можно сделать вывод, что пружина, изображенная в первом случае без деформации, имеет наименьшую потенциальную энергию, так как ее изменение длины (x) равно нулю, и формула U = (1/2)kx^2 дает значение потенциальной энергии равной нулю.